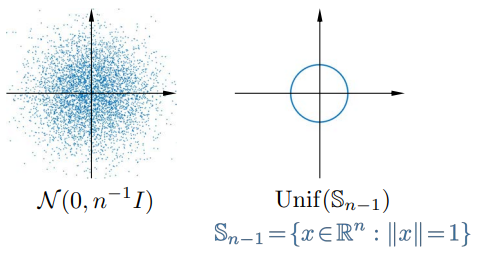零阶优化笔记

一、引言与背景

广义上的“零阶优化（Zeroth-Order Optimization, ZOO）”泛指所有仅能通过函数值进行优化的算法，亦称为无梯度（gradient-free）优化或 bandit 优化。传统方法可粗略分为以下两类：

• ​基于直接搜索的方法（Direct Search-Based Methods, DSM），例如 Nelder-Mead 单纯形法、坐标下降、模式搜索等；
• ​基于模型的方法（Model-Based Methods, MBM），例如置信域方法（Trust-region methods）等。

此外，还有两类典型的无梯度优化算法：

• ​进化算法（Evolutionary Algorithms, EA），即基于种群的通用元启发式无梯度算法，包括著名的粒子群优化（PSO）和遗传算法（GA）；
• ​贝叶斯优化（Bayesian Optimization, BO），其核心思想是将目标函数建模为一个高斯过程（Gaussian Process, GP）。

然而，这些传统无梯度方法存在两个主要缺点：
一是通常难以扩展到大规模问题；二是其中许多启发式方法缺乏收敛性保证，且难以提供系统的理论解释。

这一局限性催生了​狭义的 ZOO 算法——即作为一阶（First-Order, FO）优化方法的无梯度对应形式。这类算法通过函数值来估计梯度或随机梯度，从而复用一阶优化框架。其主要优势包括：

• ​易于实现：只需对常用梯度算法进行少量修改，将一阶梯度 Oracle 替换为基于函数值的零阶梯度估计 Oracle 即可；
• ​适用性强：在导数难以计算或不可用的场景下，仍可高效地进行近似优化；
• ​理论性能优良：其收敛速度（即分析复杂度）可与一阶梯度算法相媲美。

二、核心概念：什么是零阶优化？

零阶优化（Zeroth-Order Optimization, ZOO）是梯度无关优化（Gradient-Free Optimization）的重要分支，旨在求解如下形式的优化问题：

$$\min_{\mathbf{x} \in \mathcal{X}} f(\mathbf{x}),$$

其中目标函数 $f: \mathbb{R}^p \to \mathbb{R}$ 被视为一个黑盒（Black-Box）——我们无法获得其梯度 $\nabla f(\mathbf{x})$ 或 Hessian $\nabla^2 f(\mathbf{x})$，唯一可执行的操作是向系统输入一个点 $\mathbf{x}$ 并接收对应的函数值 $f(\mathbf{x})$。

2.1 零阶 Oracle（Zeroth-Order Oracle）

在优化理论中，Oracle 是一个标准的抽象模型，用于刻画优化算法所能获取的关于目标函数的局部信息。算法通过向 Oracle 提交查询，并接收其返回的信息，以此驱动迭代更新。

根据所返回信息的阶数，Oracle 可分为以下几类：

• 零阶 Oracle：对任意查询点 $\mathbf{x} \in \mathbb{R}^p$，返回目标函数的函数值 $f(\mathbf{x})$。
• 一阶 Oracle：返回函数值 $f(\mathbf{x})$ 及其梯度 $\nabla f(\mathbf{x})$。
• 二阶 Oracle：返回函数值、梯度及Hessian 矩阵 $\nabla^2 f(\mathbf{x})$。

零阶优化（Zeroth-Order Optimization, ZOO）问题的设定即为：优化算法仅能访问零阶 Oracle，且在有限次查询内完成优化任务。这一设定精确刻画了大量现实场景，例如：

• 黑盒函数（如商用大模型 API）仅提供输入-输出接口；
• 物理仿真器（如流体动力学模拟）的内部梯度不可解析；
• 隐私保护场景下梯度信息被禁止访问。

在此框架下，查询复杂度（Query Complexity）——即达到特定精度 $\epsilon$ 所需的函数求值次数——成为衡量 ZOO 算法效率的核心指标。

局部黑箱假设（Local Black-Box Assumption）：Oracle 是“局部”的，即其在点 $\mathbf{x}$ 处的输出仅依赖于 $\mathbf{x}$ 邻域内 $f$ 的性质，对远处的函数值进行不破坏问题类定义的扰动不会改变该输出。这保证了 Oracle 模型能用于建立与问题全局结构无关的、通用的复杂度下界。

2.2 从黑盒到梯度：核心思想与图示

ZOO 的核心思想是：通过有限次函数值查询，构造一个对真实梯度 $\nabla f(\mathbf{x})$ 的近似估计 $\hat{\nabla} f(\mathbf{x})$，从而复用一阶优化算法的框架。

如图所示：

• 左侧（FO）：优化器可直接访问白盒模型 $f$ 的梯度信息，进行高效更新。
• 右侧（ZOO）：优化器面对的是一个黑盒模型，只能通过“试探-反馈”（query-and-response）的方式间接推断函数的局部几何结构。

2.3 平滑函数 $f_r(\mathbf{x})$ 与平滑半径 $r$

由于无法直接获取 $\nabla f(\mathbf{x})$，ZOO 算法转而估计一个平滑版本（smoothed version）函数 $f_r(\mathbf{x})$ 的梯度。该平滑函数定义为：

$$f_r(\mathbf{x}) := \mathbb{E}_{\mathbf{u} \sim \mathcal{U}} \left[ f(\mathbf{x} + r \mathbf{u}) \right],$$

其中 $\mathcal{U}$ 是一个各向同性（isotropic）的随机扰动分布（见 2.4 节），$r > 0$ 被称为平滑半径（Smoothing Radius）。

• 平滑半径 $r$ 的作用：

  • 控制偏差：$f_r(\mathbf{x})$ 与 $f(\mathbf{x})$ 的偏差（及 $\nabla f_r(\mathbf{x})$ 与 $\nabla f(\mathbf{x})$ 的偏差）随 $r$ 减小而减小。
  • 引入正则性：即使 $f$ 本身不光滑，$f_r$ 几乎处处可微，从而为梯度估计提供了理论基础。
  • 权衡方差：在实践中，过小的 $r$ 会导致函数值差分被噪声淹没，因此需谨慎选择 $r$ 以平衡偏差-方差（bias-variance tradeoff）。

2.4 各向同性扰动分布

为了构造无偏的梯度估计器，扰动向量 $\mathbf{u}$ 必须服从各向同性分布，即满足：

$$\mathbb{E}[\mathbf{u}] = \mathbf{0}, \quad \mathbb{E}[\mathbf{u} \mathbf{u}^\top] = \frac{1}{p} \mathbf{I}.$$

常用的两种分布是：

1. 高斯分布 $\mathcal{N}(\mathbf{0}, p^{-1} \mathbf{I})$：

   • 优点：各分量独立，易于并行采样。
   • 缺点：无界支撑集，在有界可行域上可能产生无效查询。

2. 单位球面均匀分布 $\mathrm{Unif}(\mathbb{S}^{p-1})$：

   • 优点：$\|\mathbf{u}\| = 1$，扰动幅度固定，更适合有界问题。
   • 性质：其协方差矩阵为 $\frac{1}{p} \mathbf{I}$（由对称性与 $\sum_{i=1}^p \mathbb{E}[u_i^2] = 1$ 可得）。
   • 生成方法：若 $\mathbf{z} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$，则 $\mathbf{u} = \mathbf{z} / \|\mathbf{z}\| \sim \mathrm{Unif}(\mathbb{S}^{p-1})$。

这两种分布是构建后续所有梯度估计器（单点、两点、坐标）的基石。

三、零阶优化中的梯度估计方法

3.1 单点零阶梯度估计（Single-Point Estimator）

我们从以下单点零阶梯度估计器（single-point zeroth-order gradient estimator）开始：

$$G_f(x; r, z) = \frac{p}{r} f(x + r z) z, \quad z \sim \mathcal{Z}. \tag{2}$$

这里 $r > 0$ 是一个正参数，称为平滑半径（smoothing radius）；$z$ 是一个服从概率分布 $\mathcal{Z}$ 的 $p$ 维随机向量，我们简称其为随机扰动（random perturbation）。通常，$\mathcal{Z}$ 选择为以下分布之一：

1. 高斯分布：$\mathcal{N}(0, p^{-1} I)$。

   • 优点：变量各个分量是独立的，易于并行/分布式计算；

   • 缺点：这个分布是无界的，若 ff 定义在紧集上可能会有问题。

2. $p$ 维单位球面 $\mathbb{S}_{p-1}$ 上的均匀分布 $\mathcal{U}(\mathbb{S}_{p-1})$。

   • 优点：变量的模长是固定的，对可行域有界的情况更加适用；
   • 缺点：各分量相互依赖，不太容易分布式计算。

下面的引理描述了单点梯度估计器 (2) 的期望性质。

引理 1. 假设 $f: \mathbb{R}^p \to \mathbb{R}$ 是 $L$-光滑的。

1. 设 $\mathcal{Z}$ 为 $\mathcal{N}(0, p^{-1} I)$。则

$$\mathbb{E}_{z \sim \mathcal{Z}}[G_f(x; r, z)] = \nabla f_r(x),$$

其中 $f_r: \mathbb{R}^p \to \mathbb{R}$ 定义为

$$f_r(x) := \mathbb{E}_{y \sim \mathcal{Y}}[f(x + r y)],$$

这里 $\mathcal{Y}$ 是高斯分布 $\mathcal{N}(0, p^{-1} I)$。

2. 设 $\mathcal{Z}$ 为 $\mathrm{Unif}(\mathbb{S}_{p-1})$。则

$$\mathbb{E}_{z \sim \mathcal{Z}}[G_f(x; r, z)] = \nabla f_r(x),$$

其中 $f_r: \mathbb{R}^p \to \mathbb{R}$ 定义为

$$f_r(x) := \mathbb{E}_{y \sim \mathcal{Y}}[f(x + r y)],$$

这里 $\mathcal{Y}$ 是单位球 $\mathbb{B}_p := \{ x \in \mathbb{R}^p : \|x\| \leq 1 \}$ 上的均匀分布。

引理 1 表明，$G_f(x; r, z)$ 的期望给出了 $f$ 的一个平滑版本的梯度。下面的引理提供了 $f_r$ 和 $\nabla f_r$ 的进一步性质。

引理 2. 假设 $f$ 是凸的且 $L$-光滑的。设 $\mathcal{Z}$ 为 $\mathcal{N}(0, p^{-1} I)$ 或 $\mathrm{Unif}(\mathbb{S}_{p-1})$，并让 $f_r$ 表示对应的 $f$ 的平滑版本。那么 $f_r$ 是凸的、$L$-光滑的，并满足

$$f(x) \leq f_r(x) \leq f(x) + \frac{L r^2}{2},$$

以及

$$\|\nabla f_r(x) - \nabla f(x)\| \leq L r.$$

证明：

首先，我们证明 $f_r$ 的凸性。对于任意 $\theta \in [0,1]$ 和任意 $x_1, x_2 \in \mathbb{R}^p$，有：

$$\begin{aligned} f_r(\theta x_1 + (1 - \theta) x_2) &= \mathbb{E}_{y \sim \mathcal{Y}}[f(\theta x_1 + (1 - \theta) x_2 + r y)] \\ &= \mathbb{E}_{y \sim \mathcal{Y}}[f(\theta(x_1 + r y) + (1 - \theta)(x_2 + r y))] \\ &\leq \mathbb{E}_{y \sim \mathcal{Y}}[\theta f(x_1 + r y) + (1 - \theta) f(x_2 + r y)] \\ &= \theta \mathbb{E}_{y \sim \mathcal{Y}}[f(x_1 + r y)] + (1 - \theta) \mathbb{E}_{y \sim \mathcal{Y}}[f(x_2 + r y)] \\ &= \theta f_r(x_1) + (1 - \theta) f_r(x_2). \end{aligned}$$

这表明 $f_r$ 是凸函数。

其次，我们证明 $f_r$ 的 $L$-光滑性。令 $x_1, x_2 \in \mathbb{R}^p$ 为任意两点，则：

$$\begin{aligned} \|\nabla f_r(x_1) - \nabla f_r(x_2)\| &= \left\| \nabla_x \mathbb{E}_{y \sim \mathcal{Y}}[f(x_1 + r y)] - \nabla_x \mathbb{E}_{y \sim \mathcal{Y}}[f(x_2 + r y)] \right\| \\ &= \left\| \mathbb{E}_{y \sim \mathcal{Y}}[\nabla f(x_1 + r y) - \nabla f(x_2 + r y)] \right\| \quad (\text{交换微分与期望}) \\ &\leq \mathbb{E}_{y \sim \mathcal{Y}}[\|\nabla f(x_1 + r y) - \nabla f(x_2 + r y)\|] \quad (\text{Jensen 不等式}) \\ &\leq \mathbb{E}_{y \sim \mathcal{Y}}[L \|x_1 - x_2\|] \quad (\text{由 } f \text{ 的 } L\text{-光滑性}) \\ &= L \|x_1 - x_2\|. \end{aligned}$$

因此，$f_r$ 也是 $L$-光滑的。

接下来，我们证明第一个不等式 $f(x) \leq f_r(x) \leq f(x) + \frac{L r^2}{2}$。由于 $f$ 是凸的且 $L$-光滑的，根据一阶泰勒展开的界，对任意 $x, y$ 有：

$$f(x) + \langle \nabla f(x), r y \rangle \leq f(x + r y) \leq f(x) + \langle \nabla f(x), r y \rangle + \frac{L}{2} \|r y\|^2.$$

对上式两边关于 $y \sim \mathcal{Y}$ 取期望。因为 $\mathcal{Y}$ 是各向同性的，所以 $\mathbb{E}_{y \sim \mathcal{Y}}[\langle \nabla f(x), r y \rangle] = 0$。同时，$\mathbb{E}_{y \sim \mathcal{Y}}[\|y\|^2] = 1$（无论是高斯分布还是单位球内均匀分布均满足此性质）。于是我们得到：

$$f(x) \leq \mathbb{E}_{y \sim \mathcal{Y}}[f(x + r y)] \leq f(x) + \frac{L r^2}{2}.$$

即 $f(x) \leq f_r(x) \leq f(x) + \frac{L r^2}{2}$。

最后，我们证明第二个不等式 $\|\nabla f_r(x) - \nabla f(x)\| \leq L r$。我们有：

$$\begin{aligned} \|\nabla f_r(x) - \nabla f(x)\| &= \left\| \nabla_x \mathbb{E}_{y \sim \mathcal{Y}}[f(x + r y)] - \nabla_x f(x) \right\| \\ &= \left\| \mathbb{E}_{y \sim \mathcal{Y}}[\nabla_x f(x + r y) - \nabla_x f(x)] \right\| \quad (\text{交换微分与期望}) \\ &\leq \mathbb{E}_{y \sim \mathcal{Y}}[\|\nabla f(x + r y) - \nabla f(x)\|] \quad (\text{Jensen 不等式}) \\ &\leq \mathbb{E}_{y \sim \mathcal{Y}}[L \|r y\|] \quad (\text{由 } f \text{ 的 } L\text{-光滑性}) \\ &\leq L r \cdot \mathbb{E}_{y \sim \mathcal{Y}}[\|y\|] \\ &\leq L r \cdot \sqrt{\mathbb{E}_{y \sim \mathcal{Y}}[\|y\|^2]} \quad (\text{Jensen 不等式}) \\ &= L r. \end{aligned}$$

这里，我们使用了 $\mathbb{E}[\|y\|] \leq \sqrt{\mathbb{E}[\|y\|^2]} = 1$。因此，$\|\nabla f_r(x) - \nabla f(x)\| \leq L r$。

引理 2 限定了 $f_r - f$ 和 $\nabla f_r - \nabla f$ 的差异，我们可以看到当 $r \to 0$ 时它们都趋向于零。因此，我们可以将 $G_f(x; r, z)$ 视为 $f$ 的随机梯度，其偏差（bias）非零但可以通过平滑半径 $r$ 来控制。

方差（二阶矩）分析

我们考虑 $\mathcal{Z} = \mathrm{Unif}(\mathbb{S}^{p-1})$（高斯情形类似，但常数更复杂）。

利用泰勒展开：

$$f(\mathbf{x} + r\mathbf{z}) = f(\mathbf{x}) + \langle \nabla f(\mathbf{x}), r\mathbf{z} \rangle + \frac{1}{2} r^2 \mathbf{z}^\top \nabla^2 f(\xi) \mathbf{z},$$

其中 $\xi$ 在 $\mathbf{x}$ 与 $\mathbf{x}+r\mathbf{z}$ 之间。

代入估计器得：

$$G_f^{(1)} = \frac{p}{r} f(\mathbf{x}) \mathbf{z} + p \langle \nabla f(\mathbf{x}), \mathbf{z} \rangle \mathbf{z} + \frac{p r}{2} \mathbf{z}^\top \nabla^2 f(\xi) \mathbf{z} \cdot \mathbf{z}.$$

由于 $\mathbb{E}[\mathbf{z}] = \mathbf{0}$，第一项期望为零；但其二阶矩包含常数项 $f(\mathbf{x})^2$：

$$\begin{aligned} \mathbb{E}\left[ \|G_f^{(1)}\|^2 \right] &= \frac{p^2}{r^2} \mathbb{E}\left[ f(\mathbf{x} + r\mathbf{z})^2 \|\mathbf{z}\|^2 \right] \\ &= \frac{p^2}{r^2} \mathbb{E}\left[ f(\mathbf{x} + r\mathbf{z})^2 \right] \quad (\text{因 }\|\mathbf{z}\|=1) \\ &\geq \frac{p^2}{r^2} \left( \mathbb{E}[f(\mathbf{x} + r\mathbf{z})] \right)^2 = \frac{p^2}{r^2} f_r(\mathbf{x})^2. \end{aligned}$$

即使 $f(\mathbf{x})$ 有界（如 $|f(\mathbf{x})| \leq M$），也有：

$$\mathbb{E}\left[ \|G_f^{(1)}\|^2 \right] \geq \frac{p^2}{r^2} (f(\mathbf{x}) - Lr^2/2)^2 = \Omega\left( \frac{1}{r^2} \right).$$

关键结论：单点估计器的二阶矩下界为 $\Omega(r^{-2})$。当 $r \to 0$ 时，方差爆炸，导致梯度估计噪声极大，无法保证收敛。

相比之下，两点估计器的方差有界，故单点方法仅用于理论分析，实践中不可行。

收敛性分析

考虑基于单点估计器的 ZO-SGD 迭代：

$$\mathbf{x}_{k+1} = \mathbf{x}_k - \alpha_k G_f^{(1)}(\mathbf{x}_k; r_k, \mathbf{z}_k).$$

展开误差：

$$\begin{aligned} \mathbb{E}[\|\mathbf{x}_{k+1} - \mathbf{x}^*\|^2 \mid \mathcal{F}_k] &= \|\mathbf{x}_k - \mathbf{x}^*\|^2 - 2\alpha_k \langle \mathbf{x}_k - \mathbf{x}^*, \nabla f_{r_k}(\mathbf{x}_k) \rangle \\ &\quad + \alpha_k^2 \mathbb{E}[\|G_f^{(1)}\|^2 \mid \mathcal{F}_k]. \end{aligned}$$

前两项与两点估计器相同，但第三项（方差项）：

$$\alpha_k^2 \mathbb{E}[\|G_f^{(1)}\|^2] \geq \alpha_k^2 \cdot \frac{c p^2}{r_k^2},$$

其中 $c > 0$ 为常数。

为使偏差可控，需 $r_k \to 0$（如 $r_k = 1/\sqrt{k}$）；但此时方差项 $\propto \alpha_k^2 k$。即使取 $\alpha_k = 1/k$，方差项仍为 $\mathcal{O}(1/k)$，无法被前两项的 $- \mathcal{O}(1/k)$ 抵消，导致：

$$\sum_{k=0}^\infty \alpha_k^2 \mathbb{E}[\|G_f^{(1)}\|^2] = \infty,$$

迭代序列不收敛。

结论（Nesterov & Spokoiny, 2017）
单点 ZO 方法无法在一般光滑凸函数上保证收敛，除非对函数施加额外假设（如 $f(\mathbf{x}^*) = 0$ 以消除常数项）。即使收敛，其查询复杂度也显著差于两点方法。

3.2 两点梯度估计器 (Two-Point Gradient Estimators)

单点梯度估计器提供了一个具有非零但可控偏差的随机梯度。然而，其方差（或二阶矩）大致为 $r^{-2}$ 的量级，这可能会很大，并减缓收敛。对此，我们产生了一个流行变体——两点零阶梯度估计器（two-point zeroth-order gradient estimators），它利用两个函数值来降低方差。

存在两种版本的两点梯度估计器：

$$G_f^{(2)}(x; r, z) = \frac{p}{r} \big( f(x + rz) - f(x) \big) z,$$

和

$$\tilde{G}_f^{(2)}(x; r, z) = \frac{p}{2r} \big( f(x + rz) - f(x - rz) \big) z,$$

其中 $z \sim \mathcal{Z}$ 再次是一个随机扰动，$\mathcal{Z}$ 通常取 $\mathrm{Unif}(\mathbb{S}_{p-1})$ 或 $\mathcal{N}(0, p^{-1} I)$。

由于 $\mathcal{Z}$ 是各向同性的，我们可以看到 $G_f^{(2)}(x; r, z)$ 和 $\tilde{G}_f^{(2)}(x; r, z)$ 的期望与单点估计器相同，即：

$$\mathbb{E}_{z \sim \mathcal{Z}}[G_f^{(2)}(x; r, z)] = \mathbb{E}_{z \sim \mathcal{Z}}[\tilde{G}_f^{(2)}(x; r, z)] = \nabla f_r(x).$$

另一方面，以下引理表明，它们的二阶矩对平滑半径 $r$ 的依赖性更好。

引理 3. 假设 $f$ 是 $L$-光滑的，且 $\mathcal{Z}$ 为 $\mathcal{N}(0, p^{-1} I)$ 或 $\mathrm{Unif}(\mathbb{S}_{p-1})$。则

$$\mathbb{E}_{z \sim \mathcal{Z}}\left[ \left\| G_f^{(2)}(x; r, z) \right\|^2 \right] \leq \begin{cases} 2(p+2) \|\nabla f(x)\|^2 + \dfrac{r^2 L^2 p^2}{2} \left( \dfrac{p+6}{p} \right)^3, & \mathcal{Z} \text{ 为 } \mathcal{N}(0, p^{-1} I), \\ 2p \|\nabla f(x)\|^2 + \dfrac{r^2 L^2 p^2}{2}, & \mathcal{Z} \text{ 为 } \mathrm{Unif}(\mathbb{S}_{p-1}). \end{cases}$$

并且对 $\mathbb{E}_{z \sim \mathcal{Z}}\left[ \left\| \tilde{G}_f^{(2)}(x; r, z) \right\|^2 \right]$ 也成立相同的上界。

证明.

我们仅给出 $G_f^{(2)}(x; r, z)$ 的证明。

我们有：

$$\begin{aligned} \mathbb{E}_{z}\left[ \left\| G_f^{(2)}(x; r, z) \right\|^2 \right] &= \frac{p^2}{r^2} \mathbb{E}_{z}\left[ \left| f(x + rz) - f(x) \right|^2 \cdot \|z\|^2 \right] \\ &\leq \frac{p^2}{r^2} \mathbb{E}_{z}\left[ \left( 2 \left| f(x + rz) - f(x) - \langle \nabla f(x), rz \rangle \right|^2 + 2 \left| \langle \nabla f(x), rz \rangle \right|^2 \right) \|z\|^2 \right] \\ &= \frac{2p^2}{r^2} \mathbb{E}_{z}\left[ \left| f(x + rz) - f(x) - \langle \nabla f(x), rz \rangle \right|^2 \|z\|^2 \right] + 2p^2 \mathbb{E}_{z}\left[ \left| \langle \nabla f(x), z \rangle \right|^2 \|z\|^2 \right]. \quad (3) \end{aligned}$$

首先，我们考虑式 (3) 中的第二项。注意到：

$$\mathbb{E}_{z}\left[ \left| \langle \nabla f(x), z \rangle \right|^2 \cdot \|z\|^2 \right] = (\nabla f(x))^\top \mathbb{E}_{z}\left[ \|z\|^2 z z^\top \right] \nabla f(x).$$

• 如果 $\mathcal{Z}$ 是高斯分布 $\mathcal{N}(0, p^{-1} I)$，则：

  $$\mathbb{E}_{z}\left[ \|z\|^2 z_i z_j \right] = \sum_{k=1}^p \mathbb{E}_{z}\left[ z_k^2 z_i z_j \right] = \begin{cases} \dfrac{p+2}{p^2}, & i = j, \\ 0, & i \neq j. \end{cases}$$

  这里用到了高斯分布 $\mathcal{N}(0, 1/p)$ 的四阶矩为 $\mathbb{E}[z_i^4] = 3/p^2$。
  因此，

  $$\mathbb{E}_{z}\left[ \|z\|^2 z z^\top \right] = \frac{p+2}{p^2} I.$$

• 如果 $\mathcal{Z}$ 是 $\mathrm{Unif}(\mathbb{S}_{p-1})$，则：

  $$\mathbb{E}_{z}\left[ \|z\|^2 z z^\top \right] = \mathbb{E}_{z}\left[ z z^\top \right] = \frac{1}{p} I,$$

  这里用到了由对称性可得 $\mathbb{E}_{z}[z_i z_j] = 0$（当 $i \neq j$ 时）。

因此，第二项满足：

$$2p^2 \mathbb{E}_{z}\left[ \left| \langle \nabla f(x), z \rangle \right|^2 \cdot \|z\|^2 \right] = \begin{cases} 2(p+2) \|\nabla f(x)\|^2, & \mathcal{Z} \text{ 为 } \mathcal{N}(0, p^{-1} I), \\ 2p \|\nabla f(x)\|^2, & \mathcal{Z} \text{ 为 } \mathrm{Unif}(\mathbb{S}_{p-1}). \end{cases}$$

接下来，我们界定第一项。根据牛顿-莱布尼茨定理（Newton-Leibniz theorem）：

$$f(x + rz) - f(x) = \int_0^r \langle \nabla f(x + tz), z \rangle dt,$$

因此，

$$\begin{aligned} \left| f(x + rz) - f(x) - \langle \nabla f(x), rz \rangle \right| &= \left| \int_0^r \langle \nabla f(x + tz) - \nabla f(x), z \rangle dt \right| \\ &\leq \int_0^r \| \nabla f(x + tz) - \nabla f(x) \| \|z\| dt \\ &\leq \int_0^r Lt \|z\|^2 dt = \frac{Lr^2}{2} \|z\|^2. \end{aligned}$$

我们进而得到：

$$\begin{aligned} \frac{2p^2}{r^2} \mathbb{E}_{z}\left[ \left| f(x + rz) - f(x) - \langle \nabla f(x), rz \rangle \right|^2 \|z\|^2 \right] &\leq \frac{2p^2}{r^2} \mathbb{E}_{z}\left[ \left( \frac{Lr^2}{2} \|z\|^2 \right)^2 \|z\|^2 \right] \\ &= \frac{2p^2}{r^2} \cdot \frac{L^2 r^4}{4} \mathbb{E}_{z}\left[ \|z\|^6 \right] \\ &\leq \begin{cases} \dfrac{(p+6)^3}{p^3} \cdot \dfrac{r^2 L^2 p^2}{2}, & \mathcal{Z} \text{ 为 } \mathcal{N}(0, p^{-1} I), \\ \dfrac{r^2 L^2 p^2}{2}, & \mathcal{Z} \text{ 为 } \mathrm{Unif}(\mathbb{S}_{p-1}). \end{cases} \end{aligned}$$

这里用到了对于 $z \sim \mathcal{N}(0, p^{-1} I)$，有 $\mathbb{E}[\|z\|^6] \leq (p+6)^3 / p^3$。

综上，结合两项结果，即得引理 3 的结论。以上证明展示了方差上界的详细推导。下面，我们从一个更直观的角度来理解这个结果。

方差（二阶矩）分析

关键在于控制 $\mathbb{E}[\|\tilde{G}_f^{(2)}\|^2]$。利用泰勒展开和各向同性性，可得：

$$\begin{aligned} \mathbb{E}_{\mathbf{z}}\left[ \left\| \tilde{G}_f^{(2)}(\mathbf{x}; r, \mathbf{z}) \right\|^2 \right] &= \frac{p^2}{4r^2} \mathbb{E}_{\mathbf{z}}\left[ \left| f(\mathbf{x}+r\mathbf{z}) - f(\mathbf{x}-r\mathbf{z}) \right|^2 \|\mathbf{z}\|^2 \right] \\ &\leq \frac{p^2}{4r^2} \mathbb{E}_{\mathbf{z}}\left[ \left( 2 \langle \nabla f(\mathbf{x}), 2r\mathbf{z} \rangle + L r^2 \|\mathbf{z}\|^2 \right)^2 \|\mathbf{z}\|^2 \right] \\ &\leq 2p^2 \mathbb{E}_{\mathbf{z}}\left[ \langle \nabla f(\mathbf{x}), \mathbf{z} \rangle^2 \|\mathbf{z}\|^2 \right] + \frac{p^2 L^2 r^2}{2} \mathbb{E}_{\mathbf{z}}[\|\mathbf{z}\|^6]. \end{aligned}$$

• 项1：$\mathbb{E}[\langle \nabla f, \mathbf{z} \rangle^2 \|\mathbf{z}\|^2] = (\nabla f)^\top \mathbb{E}[\|\mathbf{z}\|^2 \mathbf{z} \mathbf{z}^\top] \nabla f$。

  • 若 $\mathcal{Z} = \mathrm{Unif}(\mathbb{S}^{p-1})$，则 $\|\mathbf{z}\| = 1$，且 $\mathbb{E}[\mathbf{z}\mathbf{z}^\top] = \frac{1}{p} \mathbf{I}$，故此项为 $\frac{1}{p} \|\nabla f\|^2$。
  • 若 $\mathcal{Z} = \mathcal{N}(\mathbf{0}, p^{-1}\mathbf{I})$，则 $\mathbb{E}[\|\mathbf{z}\|^2 \mathbf{z}\mathbf{z}^\top] = \frac{p+2}{p^2} \mathbf{I}$。

• 项2：$\mathbb{E}[\|\mathbf{z}\|^6]$ 为常数（高斯下为 $\mathcal{O}(1)$，球面上为 1）。

最终可得（以 $\mathcal{Z} = \mathrm{Unif}(\mathbb{S}^{p-1})$ 为例）：

$$\mathbb{E}\left[ \left\| \tilde{G}_f^{(2)} \right\|^2 \right] \leq 2p \|\nabla f(\mathbf{x})\|^2 + \frac{p^2 L^2 r^2}{2}.$$

关键结论：方差不再依赖 $r^{-2}$，当 $r \to 0$ 时，二阶矩趋于 $2p \|\nabla f\|^2$，有界且可控。

收敛性分析

引理3表明，任一两点梯度估计器的二阶矩在 $r \to 0$ 时不会爆炸，因此相比于单点梯度估计器，在 $r$ 较小时能实现小得多的方差。基于这一优良性质，我们可以对采用两点估计器的 ZO-SGD 进行收敛性分析。

考虑 ZO-SGD 迭代：

$$\mathbf{x}_{k+1} = \mathbf{x}_k - \alpha_k \tilde{G}_f^{(2)}(\mathbf{x}_k; r_k, \mathbf{z}_k).$$

设 $f$ 为凸且 $L$​ -光滑，存在最优解 $\mathbf{x}^*$。令 $\mathcal{F}_k = \sigma(\mathbf{x}_0, \dots, \mathbf{x}_k)$。

迭代展开：

$$\begin{aligned} \mathbb{E}\left[ \|\mathbf{x}_{k+1} - \mathbf{x}^*\|^2 \mid \mathcal{F}_k \right] &= \|\mathbf{x}_k - \mathbf{x}^*\|^2 - 2\alpha_k \langle \mathbf{x}_k - \mathbf{x}^*, \nabla f_{r_k}(\mathbf{x}_k) \rangle \\ &\quad + \alpha_k^2 \mathbb{E}\left[ \|\tilde{G}_f^{(2)}\|^2 \mid \mathcal{F}_k \right]. \end{aligned}$$

利用凸性：$\langle \mathbf{x}_k - \mathbf{x}^*, \nabla f_{r_k}(\mathbf{x}_k) \rangle \geq f_{r_k}(\mathbf{x}_k) - f_{r_k}(\mathbf{x}^*)$，
再由引理2：$f_{r_k}(\mathbf{x}) \leq f(\mathbf{x}) + \frac{L r_k^2}{2}$，
得：

$$- \langle \mathbf{x}_k - \mathbf{x}^*, \nabla f_{r_k} \rangle \leq f(\mathbf{x}^*) - f(\mathbf{x}_k) + L r_k^2.$$

又因 $f$ 光滑：$\|\nabla f(\mathbf{x}_k)\|^2 \leq 2L (f(\mathbf{x}_k) - f(\mathbf{x}^*))$，

代入方差界后可得：

$$\mathbb{E}\left[ \|\mathbf{x}_{k+1} - \mathbf{x}^*\|^2 \mid \mathcal{F}_k \right] \leq \|\mathbf{x}_k - \mathbf{x}^*\|^2 - 2\alpha_k (1 - 2\alpha_k p L) (f(\mathbf{x}_k) - f(\mathbf{x}^*)) + \alpha_k L r_k^2 + \alpha_k^2 \frac{p^2 L^2 r_k^2}{2}.$$

对 $k = 0$ 到 $K$ 累加并取全期望：

$$2 \sum_{k=0}^K \alpha_k (1 - 2\alpha_k p L) \mathbb{E}[f(\mathbf{x}_k) - f(\mathbf{x}^*)] \leq \|\mathbf{x}_0 - \mathbf{x}^*\|^2 + \sum_{k=0}^K \left( \alpha_k L r_k^2 + \alpha_k^2 \frac{p^2 L^2 r_k^2}{2} \right).$$

取 $\alpha_k = \alpha = \frac{c}{2pL}$（$0 < c < 1$），且 $r_k = r$ 为常数，则：

$$\frac{1}{K+1} \sum_{k=0}^K \mathbb{E}[f(\mathbf{x}_k) - f(\mathbf{x}^*)] \leq \frac{p L \|\mathbf{x}_0 - \mathbf{x}^*\|^2}{c(1-c)(K+1)} + \frac{L r^2}{2} \left(1 + \frac{c p}{4} \right).$$

若取 $r_k = \mathcal{O}(1/\sqrt{k+1})$，则 $\sum r_k^2 = \mathcal{O}(\log K)$，收敛项为 $\mathcal{O}(p/K + \log K / K) = \mathcal{O}(p/K)$。

最终结论（凸情形） ：
为达到 $\mathbb{E}[f(\bar{\mathbf{x}}) - f(\mathbf{x}^*)] \leq \epsilon$，需 $K = \mathcal{O}(p / \epsilon)$ 次迭代。
由于每次迭代需 2 次函数查询，总查询复杂度为 $\mathcal{O}(p / \epsilon)$。

非凸情形（一阶平稳点）

若 $f$ 非凸但 $L$-光滑，则收敛性以梯度范数衡量：

$$\frac{1}{K} \sum_{k=0}^{K-1} \mathbb{E}[\|\nabla f(\mathbf{x}_k)\|^2] \leq \mathcal{O}\left( \frac{p}{K} + r^2 \right).$$

取 $r = \mathcal{O}(1/\sqrt{K})$，则 $\mathbb{E}[\|\nabla f(\mathbf{x}_k)\|^2] \to 0$，ZO-SGD 可收敛至一阶平稳点。

单点梯度估计器与两点梯度估计器的对比总结

性质	单点估计器 $G_f^{(1)}$	两点估计器 $\tilde{G}_f^{(2)}$
期望	$\nabla f_r(\mathbf{x})$	$\nabla f_r(\mathbf{x})$
偏差	$\mathcal{O}(Lr)$	$\mathcal{O}(Lr)$
二阶矩	$\Omega(r^{-2})$	$\mathcal{O}(p |\nabla f|^2 + p^2 r^2)$
$r \to 0$ 时方差	爆炸	有界
收敛性	不保证（需强假设）	保证（凸：$\mathcal{O}(p/\epsilon)$ 查询）
实用价值	低（理论工具）	高（主流方法）
函数查询/次	1	2
迭代复杂度（凸）	（不实用）	$\mathcal{O}(p / \epsilon)$
查询复杂度（凸）	—	$\mathcal{O}(p / \epsilon)$

3.3 基于坐标的梯度估计器 (Coordinate-wise Gradient Estimator)

除了基于随机方向扰动的单点和两点梯度估计器，零阶优化还包括一类基于标准坐标基向量的方法，称为基于坐标的梯度估计器（coordinate-wise gradient estimator）。这类方法不依赖于高斯或球面均匀分布的随机向量，而是直接沿坐标轴方向进行扰动，从而估计偏导数。

形式

设 $\{ \mathbf{e}_i \}_{i=1}^p$ 为 $\mathbb{R}^p$ 中的标准基，其中 $\mathbf{e}_i$ 的第 $i$ 个分量为 1，其余为 0。坐标估计器利用前向差分或中心差分来估计每个偏导数 $\partial f / \partial x_i$。

• 完整坐标前向差分估计器（full coordinate-wise forward difference）：

  $$\hat{\nabla} f(\mathbf{x}) = \sum_{i=1}^p \frac{f(\mathbf{x} + \mu \mathbf{e}_i) - f(\mathbf{x})}{\mu} \mathbf{e}_i.$$

• 完整坐标中心差分估计器（full coordinate-wise central difference）：

  $$\hat{\nabla} f(\mathbf{x}) = \sum_{i=1}^p \frac{f(\mathbf{x} + \mu \mathbf{e}_i) - f(\mathbf{x} - \mu \mathbf{e}_i)}{2\mu} \mathbf{e}_i.$$

在实际大规模问题中，通常不会一次性估计所有 $p$ 个坐标，而是采用随机坐标下降（Stochastic Coordinate Descent）的思想，在每次迭代中随机均匀地选择一个坐标 $i \in \{1, \dots, p\}$ 进行更新，其梯度估计为：

$$\hat{\nabla} f(\mathbf{x}) = \frac{f(\mathbf{x} + \mu \mathbf{e}_i) - f(\mathbf{x} - \mu \mathbf{e}_i)}{2\mu} \mathbf{e}_i,$$

这种方式每次迭代仅需 2 次函数查询。正如综述 [Liu et al., 2020] 所指出的，当函数查询次数达到问题维度 $p$ 时，使用完整的坐标估计器 $\sum_{i=1}^p \frac{f(x+\mu e_i) - f(x)}{\mu} e_i$ 可以获得比随机方向估计更低的逼近误差，其误差阶为 $\mathcal{O}(p\mu^2)$。

理论性质与误差分析

坐标估计器的分析基于确定性的泰勒展开，其误差性质可被严格刻画。

引理 4 **(坐标估计器的偏差) 假设 $f$ 是 $L$-光滑的。对于任意坐标 $i$，中心差分估计满足：

$$\left| \frac{f(\mathbf{x} + \mu \mathbf{e}_i) - f(\mathbf{x} - \mu \mathbf{e}_i)}{2\mu} - \frac{\partial f(\mathbf{x})}{\partial x_i} \right| \leq \frac{L \mu}{2}.$$

因此，完整梯度的欧氏范数误差为：

$$\left\| \hat{\nabla} f(\mathbf{x}) - \nabla f(\mathbf{x}) \right\|_2 \leq \frac{L \mu \sqrt{p}}{2}.$$

证明：由 $L$-光滑性，$f$ 的二阶导数有界。根据泰勒定理，存在 $\xi_1 \in [\mathbf{x}, \mathbf{x}+\mu \mathbf{e}_i]$ 和 $\xi_2 \in [\mathbf{x}-\mu \mathbf{e}_i, \mathbf{x}]$ 使得

$$f(\mathbf{x} + \mu \mathbf{e}_i) = f(\mathbf{x}) + \mu \frac{\partial f(\mathbf{x})}{\partial x_i} + \frac{\mu^2}{2} \frac{\partial^2 f(\xi_1)}{\partial x_i^2},$$

$$f(\mathbf{x} - \mu \mathbf{e}_i) = f(\mathbf{x}) - \mu \frac{\partial f(\mathbf{x})}{\partial x_i} + \frac{\mu^2}{2} \frac{\partial^2 f(\xi_2)}{\partial x_i^2}.$$

两式相减并整理，利用 $\left| \frac{\partial^2 f}{\partial x_i^2} \right| \leq L$，即可得证。

在随机坐标下降的框架下，每次迭代随机选择一个坐标 $i \sim \mathrm{Unif}(\{1,\dots,p\})$，此时梯度估计器 $\hat{g} = \frac{p}{2\mu} (f(\mathbf{x} + \mu \mathbf{e}_i) - f(\mathbf{x} - \mu \mathbf{e}_i)) \mathbf{e}_i$ 是一个随机向量。其期望为：

$$\mathbb{E}_i[\hat{g}] = \sum_{i=1}^p \frac{1}{p} \cdot \frac{p}{2\mu} (f(\mathbf{x} + \mu \mathbf{e}_i) - f(\mathbf{x} - \mu \mathbf{e}_i)) \mathbf{e}_i = \hat{\nabla} f(\mathbf{x}),$$

即完整坐标梯度估计。因此，随机坐标下降可以看作是完整梯度的一个无偏随机采样，其方差来源于坐标选择的随机性，而非函数查询的噪声。这使得其在实践中具有良好的稳定性和样本效率。

关键优势：坐标估计器的误差是确定性的，不依赖于随机扰动的方差。在光滑性假设下，其估计值在每次实现中都更接近真实偏导数。当问题具有梯度稀疏性或可分离结构时，该方法尤为高效。

应用与算法实例

基于坐标的梯度估计是零阶随机坐标下降（Zeroth-Order Stochastic Coordinate Descent, ZO-SCD）算法的核心。该方法特别适用于：

• 高维但有效维度低（gradient sparsity）的问题；
• 可并行化的场景，因为不同坐标的更新可以异步进行；
• 结构化优化问题，如带有 $\ell_1$ 正则项的复合优化。

综上，零阶梯度估计的三大基本范式可总结如下：

方法	扰动类型	查询次数/次迭代	主要优势	主要考虑
单点估计器 $G_f^{(1)}$	随机方向	1	理论简洁	方差爆炸，不实用
两点估计器 $\tilde{G}_f^{(2)}$	随机方向	2	方差可控，通用性强	查询复杂度 $\mathcal{O}(p/\epsilon)$
坐标估计器	坐标基向量	$2$（随机坐标）或 $2p$（全梯度）	误差确定性小，适合稀疏/并行	全梯度查询成本高，需采样策略

四、零阶优化算法

大多数零阶优化（ZOO）算法模仿其一阶对应物（如梯度下降），采用一个统一的三步迭代框架：

1. 梯度估计 (Gradient Estimation) ：利用黑盒函数值 $f(x)$ 构造一个随机梯度估计 $\hat{g}_t$。
2. 下降方向计算 (Descent Direction Computation) ：基于当前及历史的梯度估计，计算一个下降方向 $m_t$。
3. 点更新 (Point Updating) ：根据下降方向和学习率，更新决策变量 $x_t$，并确保其满足约束条件。

这个框架是许多具体 ZO 算法的基础，包括 ZO-SGD、ZO-SCD、ZO-SVRG 等。

4.1 通用算法框架

注释：

• $\phi(\cdot)$ 是梯度估计操作，例如单点或两点估计器。
• $\psi(\cdot)$ 是下降方向更新操作，例如直接使用 $\hat{g}_t$（ZO-SGD）、取符号（ZO-signSGD）、或结合方差缩减技术（ZO-SVRG）。
• $\Pi_{\mathcal{X}}$ 是投影操作，用于处理约束优化问题（如 $\mathcal{X}$ 为闭凸集时的欧氏投影）。

4.2 常见 ZO 算法实例

无约束优化

在无约束问题 $\min_{x \in \mathbb{R}^p} f(x)$ 中，点更新步骤最为简单直接。

ZO-SGD (Zeroth-Order Stochastic Gradient Descent)

• 下降方向：$m_t = \hat{g}_t$，即直接使用当前梯度估计。
• 点更新：$x_t = x_{t-1} - \eta_t m_t$。
• 特点：这是最基础的 ZO 算法，其收敛性已在前文分析，查询复杂度为 $\mathcal{O}(p/\epsilon)$。

ZO-SVRG (Zeroth-Order Stochastic Variance Reduced Gradient)

• 下降方向：$m_t = \hat{g}_t - \tilde{g}_t + \mathbb{E}[\tilde{g}_t]$，其中 $\tilde{g}_t$ 是在某个“检查点”计算的完整梯度估计（控制变量）。
• 点更新：同 ZO-SGD。
• 特点：通过控制变量技术降低梯度估计的方差，从而加速收敛，尤其在后期迭代中效果显著。

4.2 约束优化

当优化问题包含约束 $x \in \mathcal{X}$（$\mathcal{X}$ 通常为闭凸集）时，点更新步骤必须确保新解仍在可行域内。

ZO-PSGD (Zeroth-Order Projected SGD)

• 下降方向：$m_t = \hat{g}_t$。
• 点更新：$x_t = \Pi_{\mathcal{X}}(x_{t-1} - \eta_t m_t)$，其中 $\Pi_{\mathcal{X}}$ 是到 $\mathcal{X}$ 的欧氏投影。
• 特点：约束优化中最直接的推广，适用于简单的凸约束集（如 $\ell_1/\ell_2$ 球）。

ZO-SMD (Zeroth-Order Stochastic Mirror Descent)

• 下降方向：$m_t = \hat{g}_t$。
• 点更新：基于Bregman 距离（而非欧氏距离）的镜像映射。当 Bregman 距离为 $\frac{1}{2}\|x-y\|^2$ 时，退化为 ZO-PSGD。
• 特点：通过选择合适的距离生成函数 $h(\cdot)$，可以更好地适应变量的几何结构（如概率单纯形）。

ZO-AdaMM (Zeroth-Order Adaptive Momentum Method)

• 下降方向：采用自适应动量形式（类似 Adam），即 $m_t = \beta_1 m_{t-1} + (1-\beta_1)\hat{g}_t$，并结合自适应学习率。
• 点更新：使用马氏距离（Mahalanobis distance）下的投影。
• 特点：能平衡收敛速度与精度，在黑盒对抗攻击等任务中表现出色。

4.3 复合优化

复合优化问题形式为 $\min_x f(x) + g(x)$，其中 $f$ 是光滑黑盒函数，$g$ 是非光滑但结构已知的白盒正则项（如 $\ell_1$ 范数、指示函数）。

ZO-ProxSGD / ZO-ADMM

• 下降方向：$m_t = \hat{g}_t$。
• 点更新：不再使用投影，而是调用近端算子（Proximal Operator）：$x_t = \mathrm{prox}_{\eta_t g}(x_{t-1} - \eta_t m_t)$。对于 ZO-ADMM，则引入增广拉格朗日和对偶变量进行交替更新。
• 特点：这类算法能高效处理非光滑正则项，在黑盒对抗攻击（$g$ 为 $\ell_\infty$ 球指示函数）和在线传感器管理（$g$ 为混合约束）等场景中是首选方法。

五、应用场景

零阶优化的核心价值在于处理梯度不可用或不可信的黑盒优化问题。以下几类典型场景凸显了其不可替代性：

黑盒对抗攻击与可解释性。在评估深度神经网络的鲁棒性时，攻击者或审计者往往只能通过 API 接口获取模型的输入-输出对，内部梯度信息完全不可见。在此设定下，传统的白盒攻击方法失效。零阶优化通过仅查询函数值，成功生成能诱导模型误分类的对抗样本。同样，在为复杂模型提供解释时（如回答“模型为何做出此预测？”），若模型以黑盒形式提供（如商业 API），ZO 方法能绕过梯度计算，生成模型无关的局部解释。

强化学习中的策略搜索。在无模型强化学习中，传统策略梯度方法需在高维动作空间中进行探索，其方差随轨迹长度急剧增长，导致样本效率低下。零阶策略搜索则将优化视角从动作空间转移到策略参数空间，直接通过有限差分估计策略参数的梯度。其探索复杂度仅取决于策略参数的维度，与动作空间维度和轨迹长度解耦，从而在高维任务中展现出显著优势。

在线传感器管理。在智能电网、无线传感网络等系统中，优化目标常涉及大规模矩阵的行列式（如 $\log\det$ 损失），其梯度计算需昂贵的矩阵求逆操作，成为在线优化的性能瓶颈。零阶优化通过仅依赖函数值，完全规避了显式梯度计算，为这类高维在线资源分配问题提供了高效的求解途径。

自动化机器学习（AutoML）。贝叶斯优化（BO）是 AutoML 的核心，但其内部需反复优化高斯过程（GP）的超参数，而这一过程本身依赖于对高维非凸函数求梯度。零阶优化可直接替代这一内部求解器，仅通过验证集性能（函数值）来优化超参数，从而显著加速整个 AutoML 流程。

这些应用共同表明，零阶优化已成为连接黑盒现实世界与智能优化算法的关键桥梁。

六、零阶优化（ZO）当前面临的主要问题与挑战

1. 非光滑目标函数
   大多数ZO理论依赖于目标函数的光滑性，但实际ML/DL问题常含ReLU、max等非光滑操作。虽可通过随机平滑（如双随机化）或模型基插值（如信赖域）缓解，但前者增加查询复杂度，后者引入额外计算开销。
2. 黑盒约束处理
   现有ZO方法多假设约束集（如$\mathcal{X}$）是“白盒”（可投影或已知结构）。若约束本身也是黑盒（如仅能通过函数判断可行性），则需借助障碍函数或增广拉格朗日将其融入目标函数，但会改变原问题结构并带来超参调优难题。
3. 隐私保护与分布式学习
   ZO因不传输梯度而天然具备隐私优势。然而，如何形式化地（如差分隐私）？在联邦学习中，ZO能否同时兼顾隐私性、鲁棒性（Byzantine容错）与通信效率仍是开放问题。
4. 与自动微分（AD）
   当传统AD因不可导操作（如排序、采样）失效，或需高阶导数（如元学习）时，ZO可作为替代。但如何无缝融合ZO估计与AD框架，以构建端到端可训练系统，尚缺系统性方法。
5. 离散变量优化
   现有ZO主要面向连续空间。针对离散结构（如图、文本、组合变量），简单连续松弛可能失效。亟需发展原生离散ZO算法，或设计更有效的连续-离散映射机制。
6. 紧致收敛率
   无约束凸ZO的最优查询复杂度已知（如$\mathcal{O}(d/\epsilon)$），但对于带约束/非凸/非光滑等更一般情形，最优收敛率及下界仍不明确，理论与实践存在鸿沟。

参考文献

Y. Tang, “Introduction to Zeroth-Order Optimization,” 2022.

S. Liu, P.-Y. Chen, B. Kailkhura, G. Zhang, A. O. Hero III, and P. K. Varshney, “A primer on zeroth-order optimization in signal processing and machine learning: Principles, recent advances, and applications,” IEEE Signal Processing Magazine, vol. 37, no. 5, pp. 43–54, 2020.

Y. Shu, Q. Zhang, K. He, and Z. Dai, “Refining adaptive zeroth-order optimization at ease,” in Proceedings of the 42nd International Conference on Machine Learning (ICML), 2025.

Y. Nesterov and V. Spokoiny, “Random gradient-free minimization of convex functions,” Foundations of Computational Mathematics, vol. 17, no. 2, pp. 527–566, 2017.

零阶优化算法 - 知乎

‍