梯度下降算法及其变体（上）

梯度下降法是一种优化算法，用于通过迭代调整神经网络的权重和偏置，使得损失函数的值逐步减小，最终找到一个让模型表现最好的参数组合。但为什么我们不能直接算出最优解？为什么非要这样“一步一步走”？为了解答这个问题，我把内容分成上下两篇：
上篇从最基础的起点讲起：先说清楚损失函数为什么长这样，它和概率有什么关系，为什么我们非要用它来衡量模型的好坏，最终引出梯度下降的必要。下篇则聚焦实际训练中的主流方法：从随机梯度下降法到小批量梯度下降法、动量法，再到如今大家首选的Adam算法。

损失函数

在深度学习与机器学习的实践中，我们每天都在使用损失函数：回归任务中的均方误差（MSE）、分类任务中的交叉熵、正则化项中的 L1 或 L2 惩罚……它们看似是工具箱中独立的零件，实则共享一个深层的统计学根基——概率建模与参数估计。理解这一点，不是为了炫技，而是为了在面对新问题时，能主动选择而非盲目套用损失函数。真正的模型设计者，不是调参者，而是数据生成机制的建模者。

损失函数的起源

损失函数的思想最早可追溯至 18 世纪高斯的最小二乘法。面对多次观测中微小的误差，高斯提出：应选择一个预测值，使得所有观测误差的平方和最小。这一朴素思想，成为现代回归模型的起点。

在机器学习中，我们将其抽象为：定义一个函数 $\mathcal{L}(\theta)$，衡量模型预测 $f(x; \theta)$ 与真实标签 $y$ 之间的差异，并通过优化算法寻找使该函数最小的参数 $\theta$。它的本质，是将“模型好不好”转化为一个可计算、可优化的数学目标。

随着任务多样化，损失函数不断演化：回归用 MSE 或 MAE，分类用交叉熵，生成模型用 KL 散度，排序用对比损失。但无论形式如何变化，它们都指向同一个目标：引导参数向更符合数据分布的方向调整。

最大似然估计

如果说最小二乘是经验的起点，那么最大似然估计（Maximum Likelihood Estimation, MLE）则是其理论的升华。MLE 不再问“误差多小”，而是问：“哪个参数最可能生成我们看到的数据？ ”

给定独立同分布的样本集 $\{(x^{(i)}, y^{(i)})\}_{i=1}^m$，若模型输出服从概率分布 $p(y^{(i)} | x^{(i)}; \theta)$，则联合似然为：

$$L(\theta) = \prod_{i=1}^m p(y^{(i)} | x^{(i)}; \theta)$$

为避免数值下溢，我们取对数，得到对数似然：

$$\log L(\theta) = \sum_{i=1}^m \log p(y^{(i)} | x^{(i)}; \theta)$$

最大化该式，等价于最小化其负值——即负对数似然（NLL） 。而这一目标，正是许多损失函数的原型。

高斯分布与均方误差的等价性

当假设输出 $y$ 服从以模型预测 $f(x; \theta)$ 为均值、固定方差 $\sigma^2$ 的高斯分布时：

$$y \mid x; \theta \sim \mathcal{N}(f(x; \theta), \sigma^2)$$

其概率密度函数为：

$$p(y | x; \theta) = \frac{1}{\sqrt{2\pi}\sigma} \exp\left\{ -\frac{(y - f(x; \theta))^2}{2\sigma^2} \right\}$$

代入对数似然后，忽略与 $\theta$ 无关的常数项，最大化该式等价于最小化：

$$\sum_{i=1}^m (y_i - f(x_i; \theta))^2$$

这正是均方误差（MSE）。因此，MSE 不是人为设定的“好用”函数，而是高斯噪声假设下最大似然估计的自然结果。我们选择它，是因为我们相信误差是随机、对称、小概率大偏差的。

交叉熵

在分类任务中，标签是离散的。我们不再假设高斯分布，而是用伯努利分布（二分类）或多项分布（多分类）建模。

对二分类，设真实标签 $y \in \{0,1\}$，模型输出经 sigmoid 映射为概率 $p = \sigma(f(x; \theta))$，则：

$$p(y | x; \theta) = p^y (1 - p)^{1 - y}$$

取负对数似然，得到：

$$-\log p(y | x; \theta) = -[y \log p + (1 - y) \log(1 - p)]$$

这正是二元交叉熵损失。在多分类中，配合 softmax 输出，同样导出标准的交叉熵形式。

因此，交叉熵不是“设计出来的”，而是多项分布下最大似然估计的直接推论。它要求模型不仅预测对类别，还要赋予其足够高的置信度——这正是概率建模的核心。

最大后验估计

最大似然估计依赖数据，却对参数本身无任何约束。当模型复杂或数据有限时，极易过拟合。贝叶斯学派提出：参数本身也应被视为随机变量，拥有先验信念。

最大后验估计（MAP）在 MLE 基础上引入先验分布 $p(\theta)$，根据贝叶斯定理：

$$p(\theta | \mathcal{D}) \propto p(\mathcal{D} | \theta) \cdot p(\theta)$$

取对数后，最大化后验等价于最小化：

$$-\log p(\mathcal{D} | \theta) - \log p(\theta)$$

第一项是 MLE 的负对数似然，第二项是先验带来的惩罚——这正是正则化的本质。

L2 正则：高斯先验的体现

若假设每个参数 $\theta_j \sim \mathcal{N}(0, \sigma_0^2)$，则：

$$-\log p(\theta_j) \propto \theta_j^2$$

对所有参数求和，即得 L2 正则项 $\sum_j \theta_j^2$。高斯先验鼓励参数平滑、接近零，从而抑制模型复杂度。

L1 正则：拉普拉斯先验的体现

若 $\theta_j \sim \text{Laplace}(0, b)$，则：

$$-\log p(\theta_j) \propto |\theta_j|$$

对应 L1 正则项 $\sum_j |\theta_j|$。拉普拉斯先验更偏好稀疏解——大部分参数为零，仅少数关键特征被激活。

因此，正则化不是工程技巧，而是将领域知识编码进模型的自然方式。L2 是“参数应小”，L1 是“参数应稀疏”。

贝叶斯估计

MLE 和 MAP 都输出一个“最优参数点”，但无法告诉我们模型对预测有多确定。在医疗、金融、自动驾驶等高风险场景，我们不仅需要预测值，更需要知道“它有多可能出错”。

贝叶斯估计不再寻找单一参数，而是刻画整个后验分布 $p(\theta | \mathcal{D})$。预测时，我们对所有可能参数加权平均：

$$p(y^* | x^*, \mathcal{D}) = \int p(y^* | x^*, \theta) \, p(\theta | \mathcal{D}) \, d\theta$$

这种“模型平均”天然具备抗过拟合能力，并能输出预测的不确定性。例如，在数据稀疏区域，后验分布宽广，系统可自动降低置信度。

虽然精确计算后验在神经网络中不可行，但变分推断、MCMC、Dropout 等方法正逐步实现其近似。贝叶斯方法不是替代，而是扩展——它让我们从“点估计”走向“分布理解”。

统一的认知框架

从最小二乘到交叉熵，从 L2 正则到贝叶斯估计，损失函数的演进是一条清晰的线索：它们都是不同概率假设下的最大似然或最大后验估计。

• 回归中的 MSE，是高斯噪声下的 MLE；
• 分类中的交叉熵，是伯努利/多项分布下的 MLE；
• L2 正则，是高斯先验下的 MAP；
• L1 正则，是拉普拉斯先验下的 MAP；
• 贝叶斯估计，则是完整的概率建模框架。

梯度下降法：在复杂函数中寻找出路

在深度学习中，损失函数几乎无法解析求解。神经网络由成千上万的非线性激活函数（如 ReLU、sigmoid、softmax）层层堆叠，构成一个高度非凸、高维的超越方程。我们没有“上帝视角”看清全局最优，只能从某个初始点出发，依靠局部信息一步步试探——这正是梯度下降法存在的根本意义：在无法全知的世界里，用局部梯度指引前行。

梯度

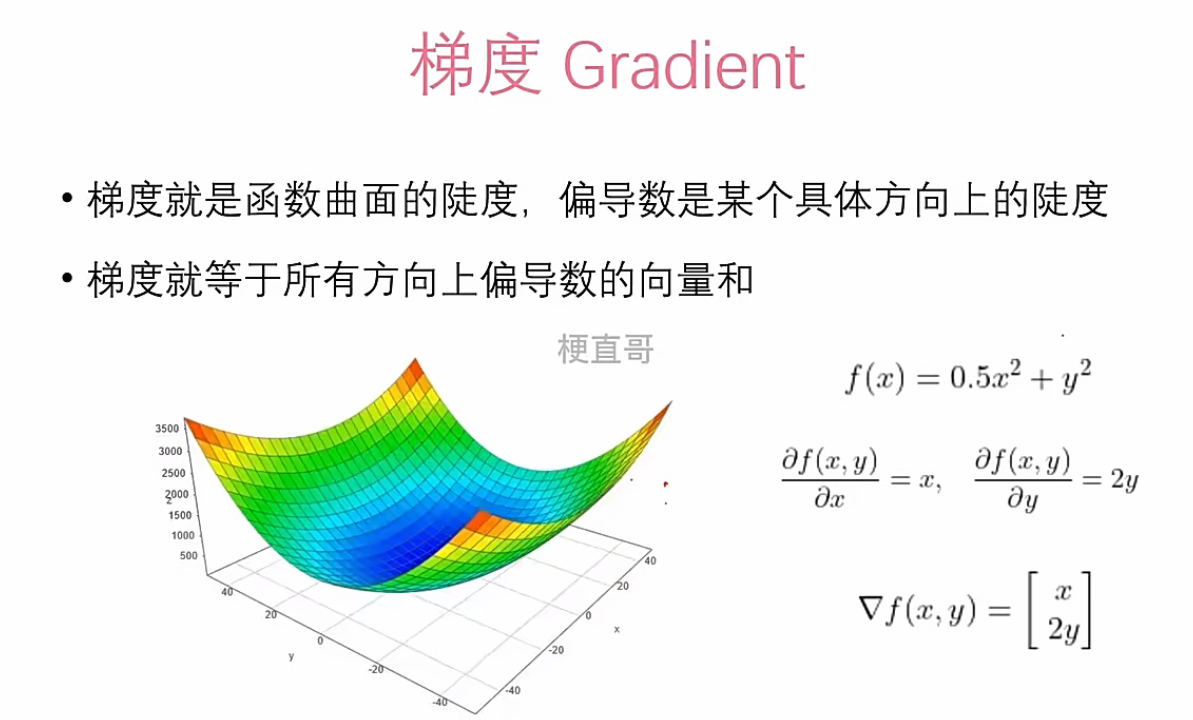
当参数为向量 $\mathbf{w} = [w_0, w_1, \dots, w_n]$ 时，损失函数 $J(\mathbf{w})$ 是一个高维曲面。梯度 $\nabla J = \left( \frac{\partial J}{\partial w_0}, \dots, \frac{\partial J}{\partial w_n} \right)$ 是该曲面上函数值增长最快的方向。我们要做的，是沿着它的反方向更新参数：

$$\mathbf{w} \leftarrow \mathbf{w} - \alpha \nabla J$$

其中 $\alpha$ 为学习率，控制更新步长。

这看似简单，却蕴含深刻的现实隐喻：我们无法预知终点，但可以知道脚下哪条路更陡。 在非凸函数中，梯度可能将我们引向局部极小值或鞍点——但这不是算法失败，而是优化本身的本质：我们追求的不是完美，而是持续改进。

链式法则

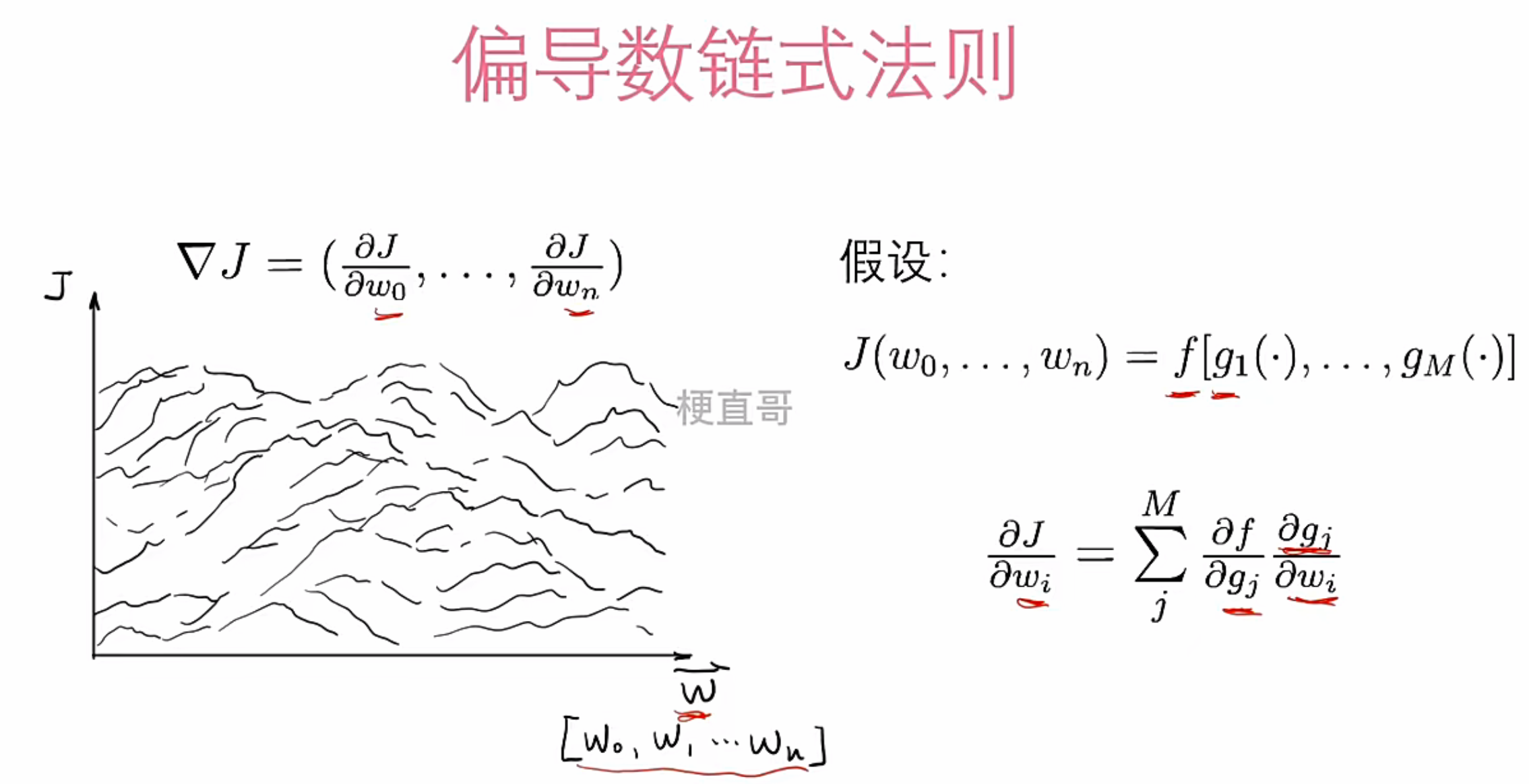
神经网络的强大源于其层级结构，但这也意味着：一个权重的变化，会通过多层非线性变换，最终影响损失。如何计算 $\frac{\partial J}{\partial w_i}$？答案是链式法则：

$$\frac{\partial J}{\partial w_i} = \sum_{j} \frac{\partial J}{\partial g_j} \cdot \frac{\partial g_j}{\partial w_i}$$

它像一台精密的回溯机器，从输出层开始，逐层分解损失对每一层参数的敏感度，最终完成梯度计算——这就是反向传播的数学内核。

现代框架如 PyTorch 自动完成这一过程，但理解它至关重要：当梯度消失或爆炸时，你不会误以为是代码错误，而是意识到——这是模型结构本身的局限，而非实现问题。

学习率与初始点

梯度决定方向，学习率决定速度。学习率过小，参数更新缓慢，收敛如同蜗行；过大，则会跨越最低点，导致震荡甚至发散。

这不只是调参技巧，更是对“节奏”的掌控：在探索与利用之间，如何找到平衡？在信息不足时，是该谨慎试探，还是大胆跃进？

另一个常被忽视的因素是初始点。同一个损失函数，从不同起点开始训练，可能收敛到完全不同的局部极小值。这不是缺陷，而是非凸优化的固有特性——结果高度依赖初始条件。

因此，我们采用 Xavier、He 等随机初始化策略，并通过多次训练或模型集成来降低对单一路径的依赖。这是一种对抗不确定性的工程智慧：我们无法控制偶然，但可以设计系统来缓冲它。

梯度下降的常用变体

标准梯度下降因计算开销大，在实际中极少使用。取而代之的是三种高效变体：

• 随机梯度下降（SGD） 每次仅用一个样本计算梯度，更新速度快但噪声大，适合数据量极大时的在线学习；
• 小批量梯度下降（Mini-batch SGD） 使用 32 或 64 个样本组成的批次，平衡了计算效率与梯度稳定性，是当前工业界的标准做法；
• 带动量的 SGD 引入历史梯度的指数加权平均，加速收敛并缓解震荡，尤其在穿越平坦区域或鞍点时表现更优。

‍