周总结（5月4日-5月11日）

一、机器学习

这一周在机器学习上完成了回归模型、决策树模型以及神经网络模型的学习。

线性回归模型

回归模型包含有线性回归以及逻辑回归。线性回归主要用于预测问题，而逻辑回归则是用于分类

1. 线性回归的原理

线性回归试图通过一个线性函数来拟合输入特征与输出之间的关系：

$$y = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n = \theta^T x$$

其中：

• $y$：输出变量（目标变量）
• $x_i$：输入特征
• $\theta_i$：模型参数（权重）

2. 目标函数（损失函数）

最小化预测值与真实值之间的均方误差（Mean Squared Error, MSE）：

$$J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2$$

3. 求解方法

• 解析解（正规方程法）：$\theta = (X^T X)^{-1} X^T y$
• 梯度下降法（Gradient Descent）等迭代优化方法

逻辑回归模型

1. 基本思想

逻辑回归虽然名字中有“回归”，但它是一个分类模型，常用于二分类问题。

它通过将线性回归的结果输入到 Sigmoid 函数中，将其映射到 [0,1] 区间，表示样本属于某一类的概率：

$$P(y=1|x;\theta) = h_\theta(x) = \frac{1}{1 + e^{-\theta^T x}}$$

最终分类结果由阈值决定（通常取0.5）：

$$\hat{y} = \begin{cases} 1 & \text{if } h_\theta(x) \geq 0.5 \\ 0 & \text{otherwise} \end{cases}$$

2. 目标函数（损失函数）

使用对数损失函数（也叫交叉熵损失）：

$$J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \left[ y^{(i)} \log(h_\theta(x^{(i)})) + (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right]$$

决策树模型

1. 基本思想

决策树是一种监督学习算法，可用于分类任务和回归任务。它通过递归选择最优特征，并根据特征值对数据集进行分割，形成一个树形结构。

• 分类树：输出类别标签（如：是否购买商品）
• 回归树：输出连续数值（如：房价）

2. 模型结构

决策树由以下几部分组成：

• 根节点（Root Node） ：整个样本集合
• 内部节点（Internal Node） ：表示一个特征或属性
• 分支（Branch） ：表示某个特征的一个取值
• 叶子节点（Leaf Node） ：代表最终的预测结果（类别或数值）

决策树的构建过程

决策树的构建是一个自上而下、分而治之的过程：

1. 选择最优特征：从所有特征中选出一个“最有区分能力”的特征。
2. 划分数据集：根据该特征的不同取值，将数据集划分为若干子集。
3. 递归建树：对每个子集重复上述步骤，直到满足终止条件（如达到最大深度、样本数太少、纯度足够高等）。

划分选择

（1）、信息增益公式[ID3]：

给定一个数据集 $D$ 和一个特征 $a$，信息增益表示为：

$$\text{Gain}(D, a) = H(D) - \sum_{v=1}^V \frac{|D^v|}{|D|} H(D^v)$$

其中：

• $H(D)$：数据集 $D$ 的经验熵（Entropy） ，表示数据集的混乱程度。
• $H(D|a)$：在已知特征 $a$ 的条件下，数据集 $D$ 的条件熵，表示使用特征 $a$ 划分后的平均混乱程度。

---

熵：对于一个样本集合 $D$，设类别有 $k$ 个，第 $k$ 类的样本占比为 $p_k$，熵为：

$$H(D) = -\sum_{k=1}^K p_k \log_2 p_k$$

条件熵：设特征 $a$ 有 $V$ 个可能的取值 $\{a^1, a^2, ..., a^V\}$，每个取值对应的子集记作 $D^v$，大小为 $|D^v|$。条件熵为：

$$H(D|a) = \sum_{v=1}^V \frac{|D^v|}{|D|} H(D^v)$$

‍

（2）基尼指数[CART]:

$$Gini(p) = 1 - \sum_{i=1}^k p_i^2$$

决策树的优化方法

• 剪枝（Pruning） ：防止过拟合

  • 预剪枝（Pre-pruning）：提前停止树的增长
  • 后剪枝（Post-pruning）：先生长完整棵树再剪枝

• 集成方法：如随机森林（Random Forest）、梯度提升树（GBDT）、XGBoost 等，利用多个决策树组合提高性能

神经网络模型

​

神经网络（Neural Network）是一种通过模拟神经元之间的连接关系，从数据中自动学习特征和规律的模型。神经网络能够自动学习复杂非线性关系并端到端提取特征，在图像、语音和自然语言处理等领域表现优异，但其依赖大量数据与计算资源，训练耗时且调参困难，模型可解释性较差。

一、神经网络的基本原理

1. 基本组成单元：神经元（Neuron）

一个神经元接收多个输入信号，每个信号都有一个权重（Weight），经过加权求和并通过一个激活函数（Activation Function）处理后输出：

$$y = f\left( \sum_{i=1}^{n} w_i x_i + b \right)$$

• $x_i$：输入特征
• $w_i$：对应权重
• $b$：偏置项（Bias）
• $f(\cdot)$：激活函数
• $y$：输出结果

2. 神经网络的结构

典型的神经网络由以下几层构成：

层级名称	功能说明
输入层（Input Layer）	接收原始数据输入，如图像像素、文本向量等
隐藏层（Hidden Layers）	若干层，用于提取数据的高阶特征，层数越多越“深”
输出层（Output Layer）	输出最终预测结果，如分类标签或回归值

二、神经网络的工作流程

神经网络的训练过程主要分为两个阶段：

1. 前向传播（Forward Propagation）

输入数据逐层传递，每一层计算加权和并应用激活函数，直到输出层得到预测结果。

例如，在第 $l$ 层：

$$z^{(l)} = W^{(l)} a^{(l-1)} + b^{(l)}$$

$$a^{(l)} = f(z^{(l)})$$

其中：

• $z^{(l)}$：线性组合结果
• $a^{(l)}$：该层的输出（激活值）

2. 反向传播（Backward Propagation）

根据预测误差，从输出层反向传播到输入层，使用梯度下降法更新参数（权重和偏置）以最小化损失函数。

损失函数（Loss Function）：

• 分类任务常用交叉熵损失（Cross Entropy Loss）：

  $$L = -\sum_{i} y_i \log(\hat{y}_i)$$

• 回归任务常用均方误差（MSE）：

  $$L = \frac{1}{2} \sum_{i} (y_i - \hat{y}_i)^2$$

参数更新公式（梯度下降）：

$$W^{(l)} := W^{(l)} - \eta \frac{\partial L}{\partial W^{(l)}}$$

$$b^{(l)} := b^{(l)} - \eta \frac{\partial L}{\partial b^{(l)}}$$

• $\eta$：学习率（Learning Rate）
• $\frac{\partial L}{\partial W}, \frac{\partial L}{\partial b}$：损失对参数的梯度

三、激活函数（Activation Functions）

激活函数引入非线性能力，使神经网络可以拟合复杂函数。

函数名	公式	特点
Sigmoid	$f(x) = \frac{1}{1+e^{-x}}$​	输出在 (0,1)，适合二分类输出层，但易梯度消失
Tanh	$f(x) = \tanh(x)$​	输出在 (-1,1)，比Sigmoid中心对称，收敛更快
ReLU（最常用）	$f(x) = \max(0, x)$​	简单高效，缓解梯度消失问题
Softmax	$f(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}}$​	多分类输出层用，输出概率分布

四、训练流程总结（完整步骤）

1. 初始化参数：随机初始化权重和偏置
2. 前向传播：计算每层输出，直到得到预测值
3. 计算损失：比较预测值与真实值的差距
4. 反向传播：计算损失对参数的梯度
5. 更新参数：使用梯度下降更新权重和偏置
6. 重复迭代：直到达到最大训练轮数（Epoch）或损失收敛

二、算法

本周算法学习的是排序和查找

（1）排序：sort​

在 C++ 中，排序主要通过标准库函数 std::sort​ 实现。该函数定义在头文件 <algorithm>​ 中，可以对数组、vector​ 等容器进行高效排序。

基本用法：

#include <algorithm>
#include <vector>

// 对数组排序
int arr[N];
std::sort(arr, arr + N);  // 默认升序

// 对 vector 排序
std::vector<int> vec;
std::sort(vec.begin(), vec.end());  // 同样默认升序

自定义排序规则（Compare 函数）

若需要自定义排序规则，可以通过传入一个比较函数作为第三个参数：

bool compare(int lhs, int rhs) {
    // 自定义排序逻辑
}

• ​compare​ 函数必须返回布尔值；
• 参数类型应与容器元素类型一致；
• 若希望 lhs​ 排在 rhs​ 前面，返回 true​，否则返回 false​。

示例：奇数从大到小，偶数从小到大排序

以下示例实现了将整型数组中的奇数按降序排列，偶数按升序排列：

bool compare(int lhs, int rhs) {
    if (lhs % 2 == 1 && rhs % 2 == 0) {
        return true;  // 奇数排在偶数前面
    } else if (lhs % 2 == 1 && rhs % 2 == 1) {
        return lhs > rhs;  // 奇数之间降序
    } else if (lhs % 2 == 0 && rhs % 2 == 0) {
        return lhs < rhs;  // 偶数之间升序
    } else {
        return false;  // 偶数不排在奇数前面
    }
}

int main() {
    int arr[10];
    for (int i = 0; i < 10; ++i) {
        scanf("%d", &arr[i]);
    }

    std::sort(arr, arr + 10, compare);

    for (int i = 0; i < 10; ++i) {
        printf("%d ", arr[i]);
    }
    printf("\n");

    return 0;
}

📌 注意事项

• ​sort​ 的时间复杂度为 O(n log n) ，使用的是混合排序算法（IntroSort），效率高。
• 数组名 arr​ 在作为参数传递时会退化为指针，因此 arr + 10​ 表示数组末尾的下一个位置。
• 对 vector​ 使用时，推荐使用 vec.begin()​ 和 vec.end()​ 来指定范围：

std::sort(vec.begin(), vec.end(), compare);

（2）查找

1. 二分查找（Binary Search）

适用于有序数据结构（如排序数组、vector​），通过不断缩小查找范围快速定位目标值。

• 优点：查找效率高，空间利用率好。
• 缺点：仅适用于静态或不频繁修改的数据，插入/删除代价较高。

时间复杂度：

操作	时间复杂度
查找	O(log n)
插入/删除	O(n)

2. map​ 查找（有序）

底层实现为红黑树，自动按键排序，适用于需要按顺序访问键值对的场景。

• 优点：支持有序遍历，可直接使用迭代器获取最小/最大键等。
• 缺点：额外空间开销，插入/删除较慢。

时间复杂度：

操作	时间复杂度
查找、插入、删除	O(log n)

3. unordered_map​ 查找（无序）

底层实现为哈希表，无序但查找速度极快，适合只关心是否存在或统计频率的场景。

• 优点：平均时间复杂度为 O(1)，适合大数据量下高效查找。
• 缺点：最坏情况下退化为 O(n)，且不保证元素顺序。

时间复杂度：

操作	平均复杂度	最坏复杂度
查找、插入、删除	O(1)	O(n)

🌰 问题：找出出现次数超过一半的元素

给定一个整型数组 nums​，请找出其中出现次数超过数组长度一半的元素。
假设数组非空，且一定存在这个数。

示例：

输入: [1,2,3,2,2,2,5,4,2]
输出: 2

方法一：使用 map​ 统计频率

int majorityElement(vector<int>& nums) {
    map<int, int> freq;
    for (int num : nums) {
        ++freq[num];
        if (freq[num] > nums.size() / 2)
            return num;
    }
    return -1; // 不会执行到这里
}

• 特点：有序结构，便于调试查看键值顺序；
• 时间复杂度：O(n log n)；
• 适用场景：需要保持键顺序时使用。

方法二：使用 unordered_map​​ 统计频率（推荐）

int majorityElement(vector<int>& nums) {
    unordered_map<int, int> freq;
    for (int num : nums) {
        ++freq[num];
        if (freq[num] > nums.size() / 2)
            return num;
    }
    return -1;
}

• 特点：平均 O(1) 的查找和插入，效率更高；
• 时间复杂度：O(n)；
• 适用场景：仅需查找，不需要顺序性，适合大规模数据。

方法三：排序 + 取中间值

int majorityElement(vector<int>& nums) {
    sort(nums.begin(), nums.end());
    return nums[nums.size() / 2];
}

• 原理：由于该元素出现次数超过一半，排序后它必定位于中间位置；
• 特点：无需额外空间，适合内存敏感的场景；
• 时间复杂度：O(n log n)；
• 空间复杂度：O(1)（若允许修改原数组）；

三、拓扑

目前我学到了持续同调（Persistent Homology） ，这是拓扑数据分析中的一个核心概念。它用于研究数据在不同尺度下的拓扑特征变化，尤其是如何从简单结构演化出复杂的拓扑特征，并追踪这些特征的“出生”和“死亡”。

1. 基本背景与动机

持续同调的核心目标是理解数据集在多尺度下表现出的拓扑性质。通常我们面对的数据可能是点云或图像，它们本身没有显式的几何结构，但可以通过构造滤子序列（filtration）将它们映射到一个具有层次结构的空间中，从而捕捉其连通性、洞的数量等信息。

例如，在分析一个实值函数 $f: M \to \mathbb{R}$ 时，可以定义其次水平集（sublevel set）：

$$M_a = f^{-1}(-\infty, a] = \{x \in M \mid f(x) \leq a\}$$

随着参数 $a$ 增大，$M_a$ 逐渐包含更多的数据，形成一个嵌套增长的拓扑空间序列（filtration）。通过计算每个阶段的同调群，我们可以观察拓扑特征的变化过程。

2. 持续图（Persistence Diagram）

持续图是一种二维平面上的可视化工具，用于表示所有拓扑特征的出生与死亡时间。图上的每个点 $(b, d)$ 对应一个 $p$-维持续同调类，横坐标表示出生时间，纵坐标表示死亡时间。

• 如果 $b = d$，则该点位于对角线 $y = x$ 上，表示该特征瞬间出现又消失。
• 点离对角线越远，说明该特征越“持久”，即在数据中更稳定地存在。
• 图中还可能包含多个点，代表不同维度的拓扑特征（如连通区域、环、空洞等）。

​

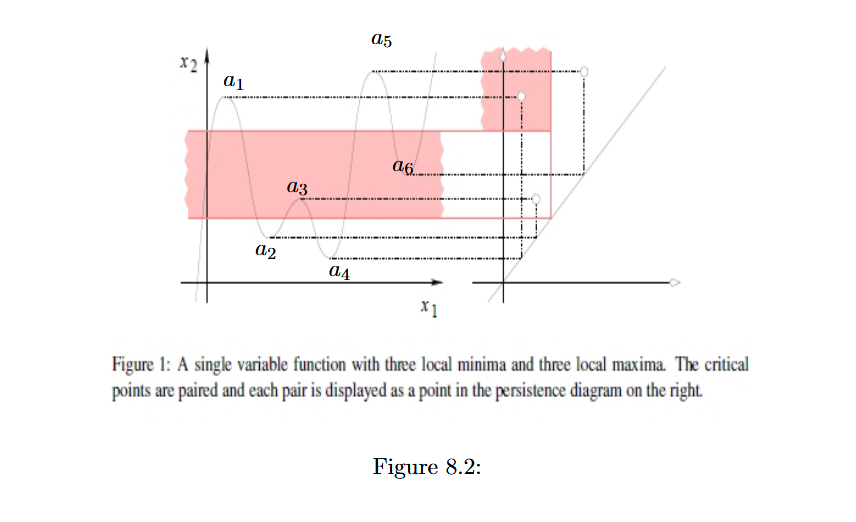
3. 持续同调的算法实现：

（1）构建联合边缘矩阵

对于每个单纯形 $\sigma_i$，构造一个边界矩阵 $D[i, j]$，其中：

$$D[i, j] = \begin{cases} 1 & \text{若 } \sigma_i \text{ 是 } \sigma_j \text{ 的一个面且系数为1} \\ 0 & \text{否则} \end{cases}$$

这个矩阵记录了单纯复形之间的边界关系。

（2）矩阵的性质

• 稀疏性 ：由于每个单纯形只可能有几个低维的面，所以大多数位置为 0。
• 上三角结构 ：如果单纯形按滤子顺序排列，则矩阵具有近似上三角的形式，因为后面的单纯形不会成为前面的面。
• 模 2 运算 ：在拓扑数据分析中，通常使用 Z2 域（即二进制域），因此所有的运算都在模 2 下进行。

（3）高斯消元法求解

联合边界矩阵的关键用途是用于高斯消元（Gaussian elimination） ，以提取持续对（persistence pairs）。具体步骤如下：

步骤 1：初始化

从最左边一列开始处理，每列代表一个单纯形。

步骤 2：寻找主元（pivot）

对于当前列 j，找到最低非零行索引 low(j)，即该列中最后一个非零元素所在的行号。

步骤 3：消元

如果存在另一列 j′<j，使得 low(j′)=low(j)，则将第 j′ 列加到第 j 列（模 2 加法），使得当前列的主元变为 0。

步骤 4：标记持续对

当某一列无法再被其他列消去时，就形成一个持续对 (birth,death)，表示某个拓扑特征在何时出生、何时死亡。

（4）Betti 数与持续性

定义了一个衡量持续性的指标：

$$\mu_{i,j}^p = (\beta_{i,j}^p - \beta_{i,j+1}^p) - (\beta_{i-1,j}^p - \beta_{i-1,j+1}^p)$$

其中 $\beta_{i,j}^p = \text{rank}(H_i^j)$ 是第 $i$ 到第 $j$ 阶段的 $p$-维 Betti 数。这个公式用于量化某个拓扑特征在特定区间内的稳定性。

四、下一周计划

后两周即将参加GXCPC，以算法的学习为主，机器学习也继续推进，同时要在翻译上下点功夫。本周计划将算法推进到第6章的递归和分治，机器学习进行到第七章的贝叶斯分类，同时活动有：周五要去深圳参观哈工深，周日还需要进行拓扑学习的分享。因此本周需要我合理安排学习时间，提高学习效率。

‍