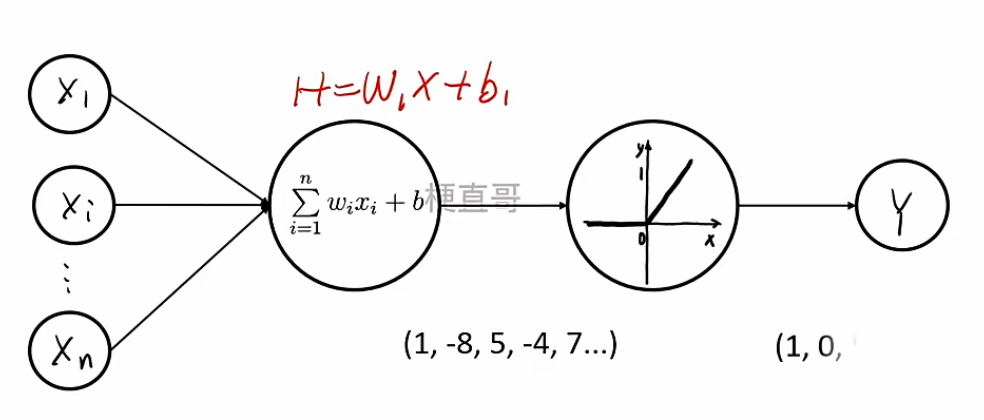神经网络基础:从感知机到反向传播
1. 神经元模型
神经网络的基本单元是神经元(Neuron) ,其数学形式为:
y=f(i=1∑nwixi+b)=f(w⊤x+b)
其中:
- x∈Rn 为输入向量;
- w∈Rn 为权重向量;
- b∈R 为偏置项;
- f(⋅) 为激活函数(Activation Function),用于引入非线性。
该模型本质上是线性变换 w⊤x+b 与非线性激活函数的组合。若省略激活函数,则整个网络退化为线性模型。单个神经元模型,也常被称为“感知器”(Perceptron)。
2. 神经网络结构
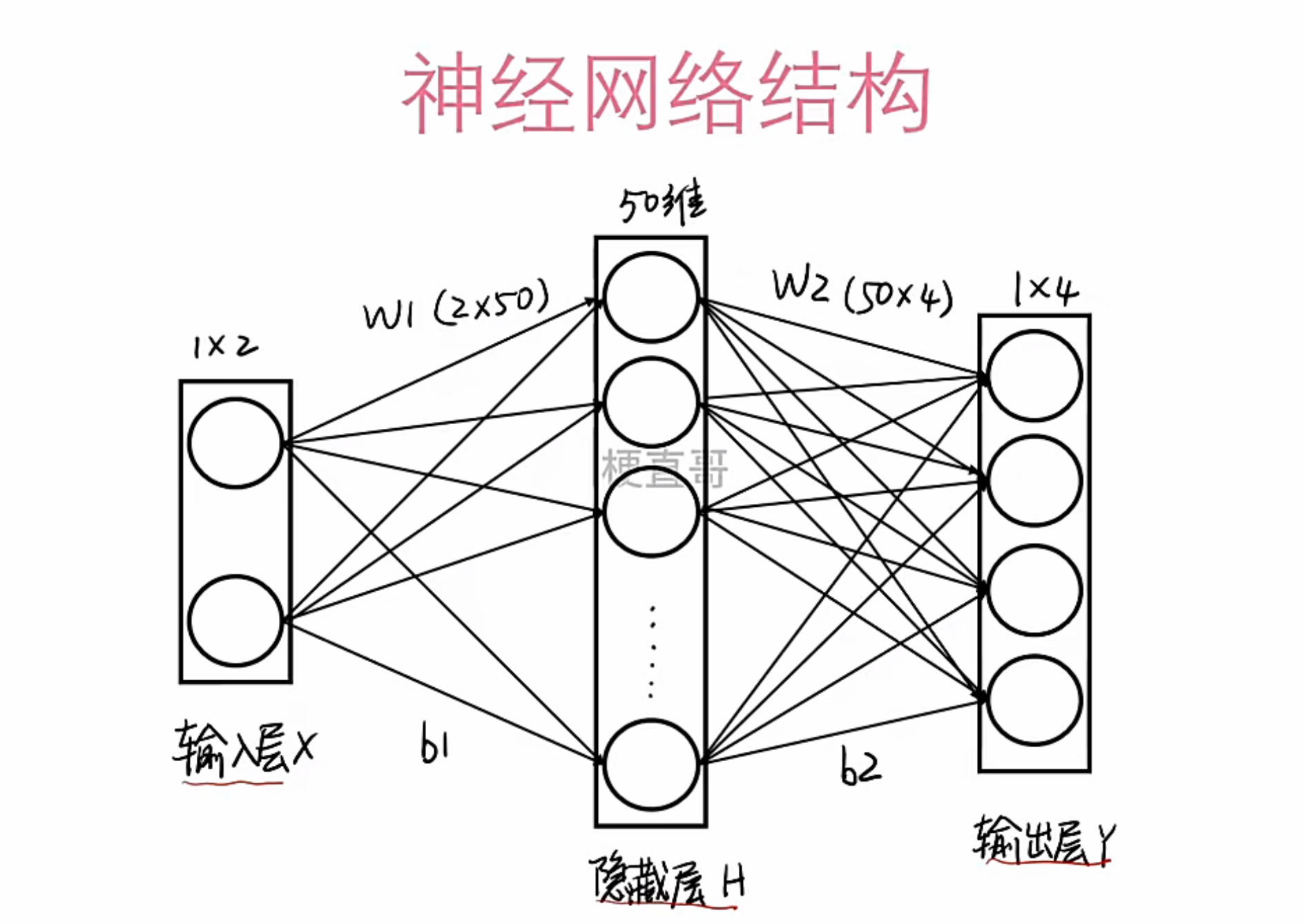
多个神经元前后相连,就构成了神经网络。 一个典型的前馈神经网络由以下三层构成:
- 输入层(Input Layer):接收原始特征向量 x∈Rd;
- 隐藏层(Hidden Layer(s)):执行特征提取与非线性变换;层数和每层神经元数量并非越多越好,过多容易导致过拟合,泛化能力差。
- 输出层(Output Layer):给出最终的预测结果,比如分类标签或回归值。
设第 l 层的输出为 h(l),则前向传播过程可表示为:
h(l)=f(l)(W(l)h(l−1)+b(l))
其中 W(l) 和 b(l) 分别为第 l 层的权重矩阵与偏置向量。
3. 为何需要非线性?——多层感知机(MLP)的动机
若所有层均为线性变换,则无论网络深度如何,整体仍等价于单一线性映射。例如,对两层网络:
hy=W1x+b1=W2h+b2=W2(W1x+b1)+b2=(W2W1)x+(W2b1+b2)
结果仍为仿射变换。
如果神经网络只有线性变换,那无论堆叠多少层,其效果都等同于一个单层线性模型,这就是所谓的“退化”问题。为了赋予网络强大的表达能力,我们必须在每一层线性计算后加入激活函数层。因此,必须引入非线性激活函数,才能使网络具备拟合复杂函数的能力。
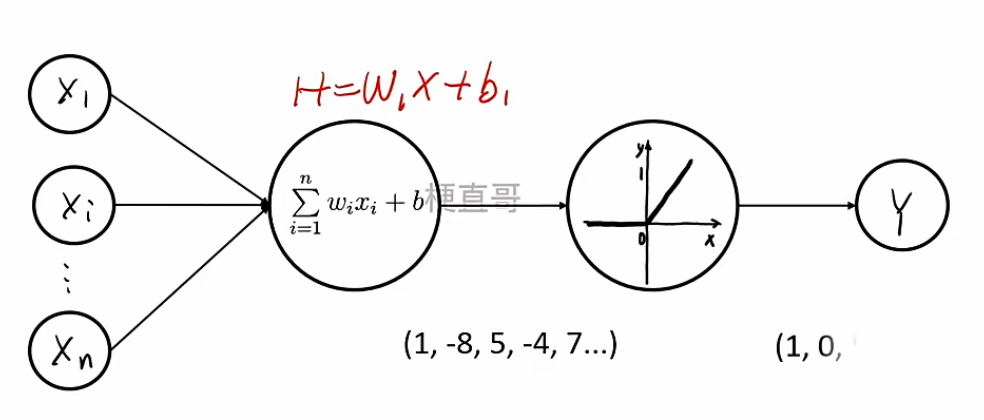
多层感知机(Multilayer Perceptron, MLP)即是在隐藏层中引入激活函数的前馈神经网络,是现代深度学习模型的基础。
4. 激活函数层
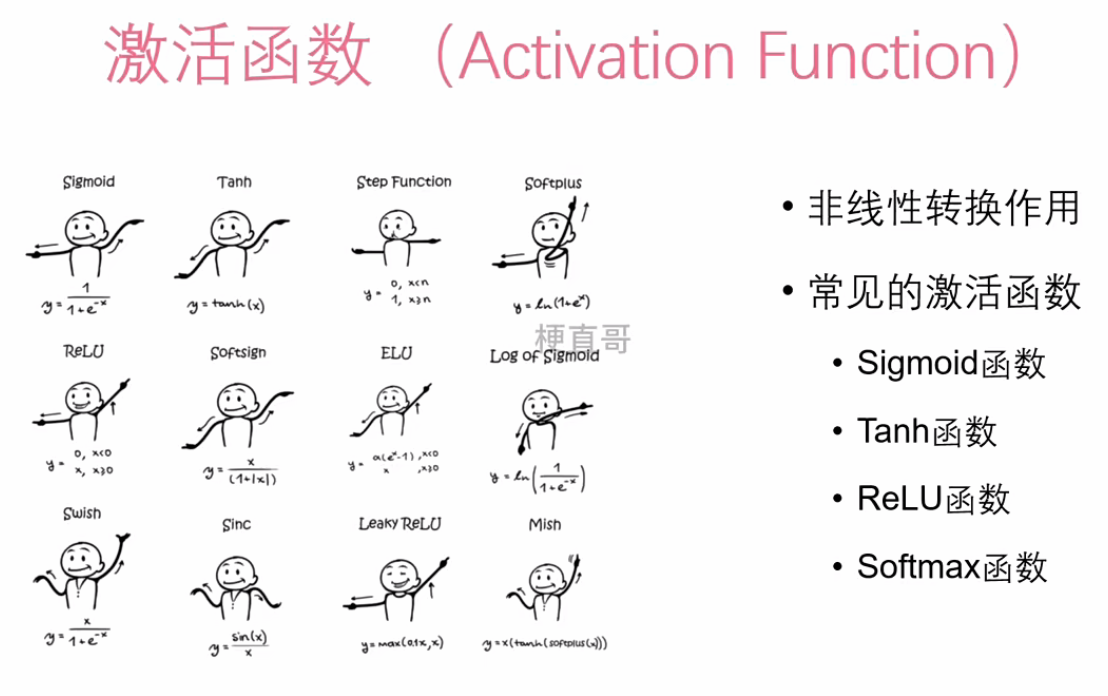
(1) Sigmoid 函数
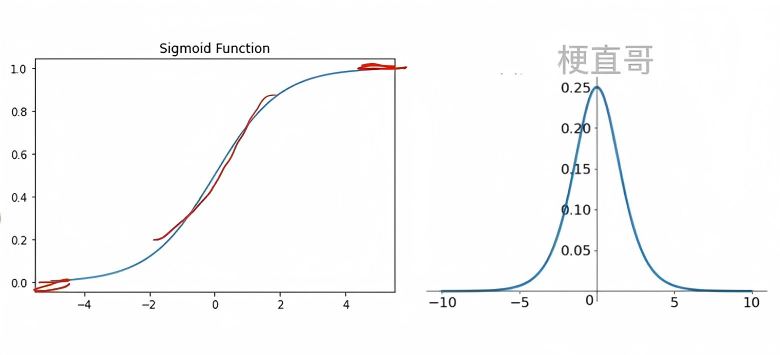
σ(x)=1+e−x1
- 输出范围:(0,1);
- 常用于二分类输出层;
- 缺点:梯度饱和(梯度消失);输出非零中心:0.5。
(2) Tanh 函数
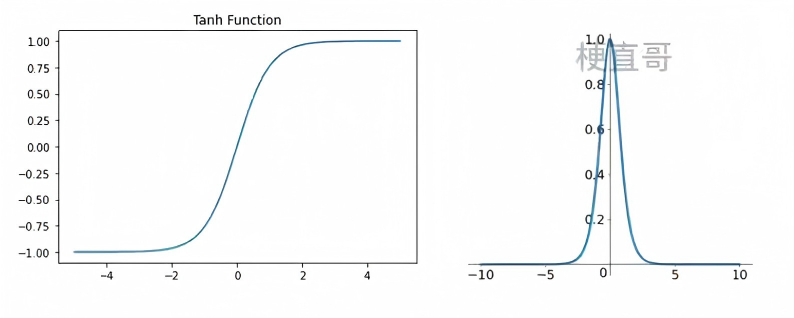
tanh(x)=ex+e−xex−e−x
- 输出范围:(−1,1);
- 零中心,收敛通常快于 Sigmoid;
- 仍存在梯度消失问题。
(3) ReLU 函数(Rectified Linear Unit)
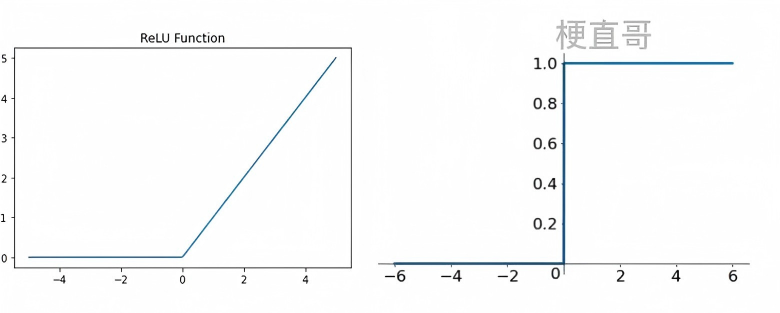
ReLU(x)=max(0,x)
- 计算高效,无指数运算;
- 梯度在 x>0 时恒为 1,缓解梯度消失;
- 缺点:存在“Dead ReLU”问题(负输入导致神经元永久失活)。
ReLU 及其变体(如 Leaky ReLU、ELU)是当前深度网络隐藏层的默认选择。
(4) Softmax 函数(用于多分类输出层)
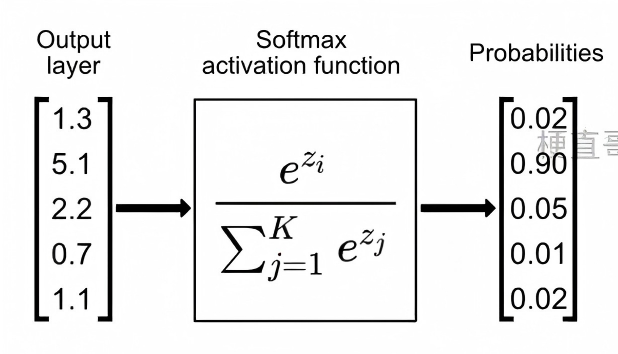
Softmax(zi)=∑j=1Kezjezi,i=1,…,K
- 将任意实数向量 z∈RK 映射为概率分布;
- 输出满足 ∑i=1KSoftmax(zi)=1 且 Softmax(zi)∈(0,1);
- 通常与交叉熵损失联合使用。
5 . Softmax层与训练目标
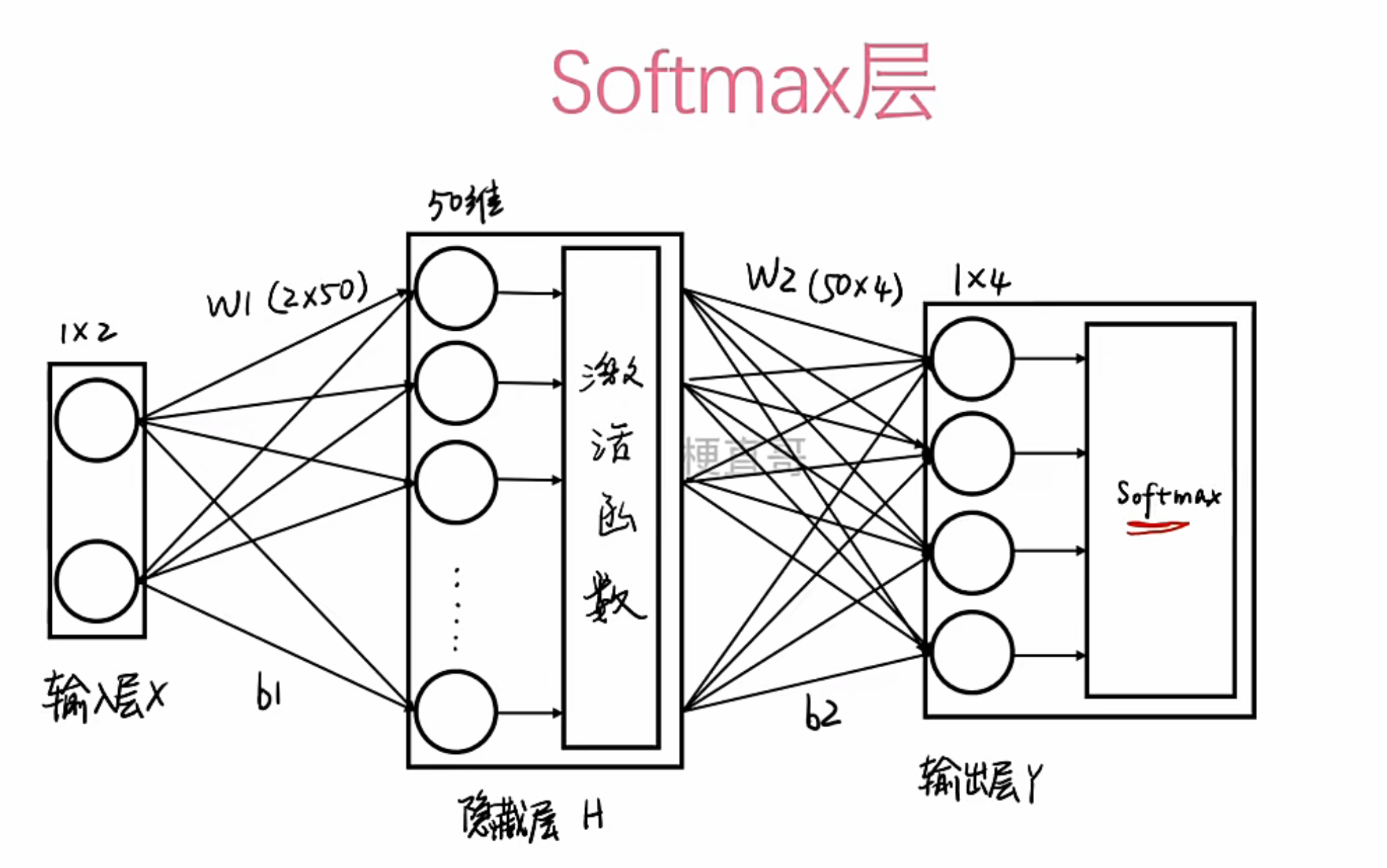
Softmax层
Softmax层:通常用于多分类任务的输出层。它的作用是将网络最后一层的原始输出(可能是任意实数)归一化成一个概率分布。这样,每个输出节点的值都在[0, 1]之间,且所有值之和为1。数值最大的那个节点,就代表了模型预测的类别。
我们使用损失函数 (Loss Function) 来量化预测结果与真实标签之间的差距。对于分类任务,常用交叉熵损失(Cross-Entropy Loss),预测越准确(概率越接近1),损失值越小。:
L=−i=1∑Kyilog(y^i)
其中:
- y∈{0,1}K 为 one-hot 真实标签;
- y^=Softmax(z) 为模型预测概率。
训练目标是最小化损失函数 L,通过反向传播(Backpropagation)与梯度下降更新参数 {W(l),b(l)}。
6 . 反向传播:让网络自己学习
有了损失函数,我们就有了优化目标:最小化损失。那么如何调整网络中的海量参数(权重W和偏置b)呢?答案就是反向传播算法 (Backpropagation) 。
反向传播的核心思想是 : 利用梯度下降法。想象损失函数是一个“山丘”,我们的目标是找到最低点(全局最小值)。反向传播就像一个登山者,沿着山坡最陡峭的下坡方向(负梯度方向)一步步前进,不断更新W和b的值,直到找到最低点。
步骤:从输出层的损失开始,根据链式法则,将误差一层层地反向传递回前面的每一层,从而计算出每一层参数的梯度,并据此更新参数。
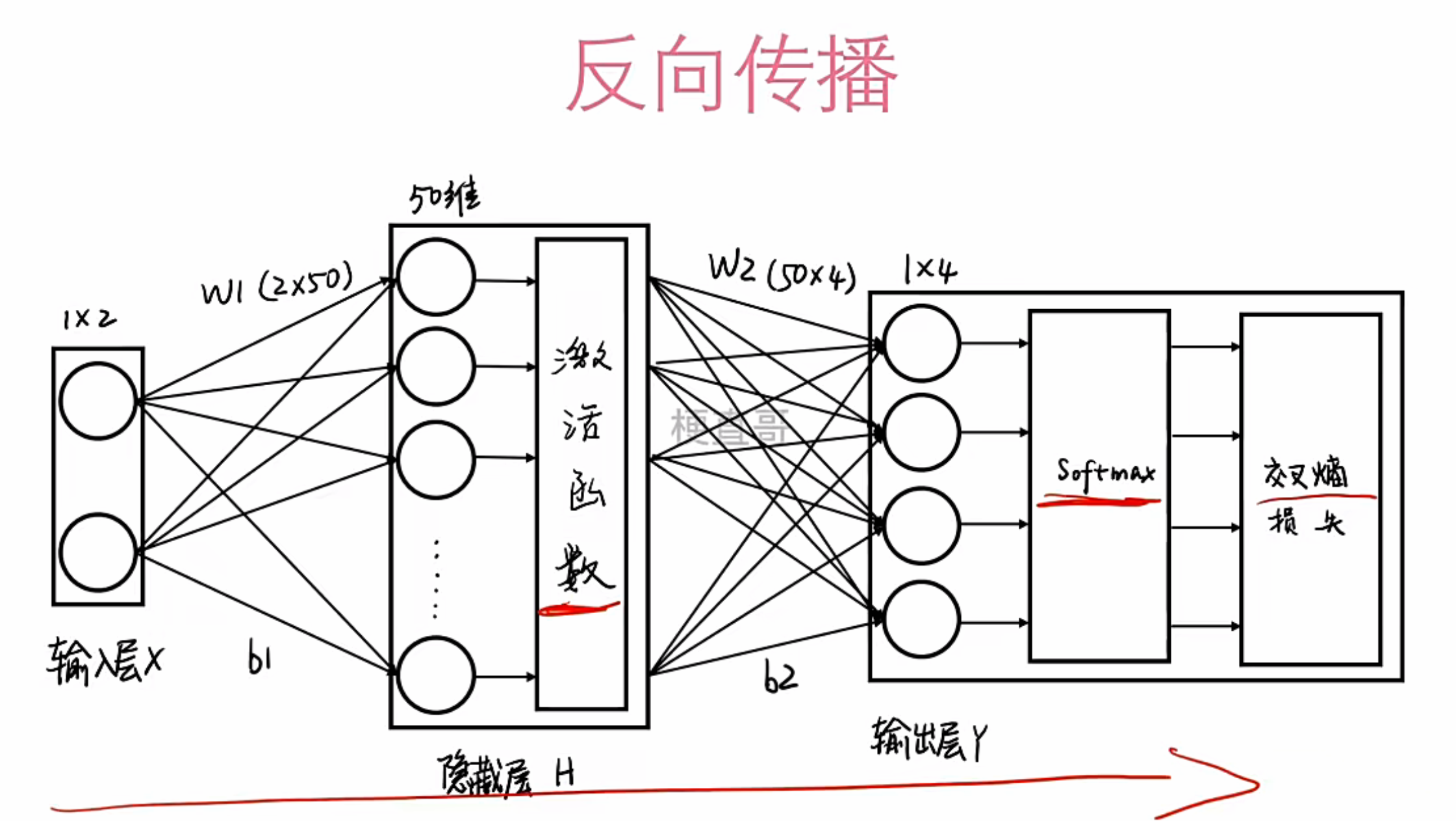
红色箭头清晰地标示了信息流的方向:从输入到输出是“前向传播”,从损失到输入是“反向传播”。
总结
神经网络的学习之旅,可以概括为以下几个步骤:
- 前向传播:数据从输入层进入,经过层层线性变换和激活函数处理,最终到达输出层。
- 计算损失:输出层的结果经过Softmax等处理后,与真实标签对比,通过损失函数计算出当前的“错误程度”。
- 反向传播:根据损失值,利用梯度下降法,从后往前计算并更新网络中所有的权重和偏置参数。
- 迭代优化:重复以上过程,直到损失值足够小,或者达到预设的训练轮数。
6.前向传播与反向传播

(1)神经网络为何需要前向与反向传播
神经网络本质上是一种参数化的非线性函数逼近器。其目标是通过调整内部参数(权重与偏置),使得对输入样本的预测尽可能接近真实标签。这一目标的实现依赖两个关键过程:
- 前向传播(Forward Propagation):用于计算模型在当前参数下的预测输出;
- 反向传播(Backpropagation):用于计算损失函数对所有参数的梯度,从而指导参数更新。
若仅进行前向计算而无法有效更新参数,则网络无法“学习”。早期的感知机模型因缺乏有效的多层参数更新机制而受限。直到 1986 年,Hinton 等人提出反向传播算法,才使得多层非线性网络的端到端训练成为可能,由此奠定了现代深度学习的基础。
(2)前向传播:从输入到预测
前向传播描述数据在网络中的流动过程。设第 l 层的输入为 h(l−1),其输出为:
z(l)=W(l)h(l−1)+b(l),h(l)=f(l)(z(l))
其中:
- W(l) 为权重矩阵,
- b(l) 为偏置向量,
- f(l) 为激活函数。
若无激活函数(即 f(l) 为恒等映射),则无论网络深度如何,整体仍等价于单一线性变换:
y=W(L)⋯W(1)x+常数项
此类模型无法拟合非线性可分问题(如异或、环形分布等)。因此,激活函数的引入是神经网络具备表达能力的关键,它使网络能够将输入映射到高维非线性空间,在该空间中原本不可分的数据变得线性可分。
对于 K 类分类任务,输出层通常采用 Softmax 激活函数:
y^k=∑j=1Kezj(L)ezk(L),k=1,…,K
该变换将原始输出归一化为概率分布,便于后续损失计算与类别预测。
(3) 损失函数:量化预测误差
训练的目标是最小化模型预测与真实标签之间的差距。以均方误差(MSE)为例:
E=21k=1∑K(y^k−dk)2
其中 dk 为真实标签(one-hot 编码),y^k 为模型预测值。因子 21 用于简化求导结果。
由于损失函数 E 是关于网络参数 {W(l),b(l)} 的高度非线性函数,通常无解析解,需借助数值优化方法(如梯度下降)迭代求解。为此,必须高效计算 ∂wji∂E 等偏导数——这正是反向传播的核心任务。
(4)反向传播:基于链式法则的梯度计算
4.1 动机
若直接对 E 关于每个参数求偏导,计算复杂度随网络规模指数增长。反向传播通过动态规划思想与链式法则,将梯度计算分解为局部可复用的子问题,实现高效、自动的梯度推导。
4.2 链式法则推导(以两层网络为例)
定义变量:
-
隐藏层神经元 j 的加权输入:xj=∑iwjiyi+bj
-
隐藏层输出:yj=f(xj),f 为可导激活函数(如 Sigmoid)
-
输出层预测:y^k
-
真实标签:dk
-
损失函数:E=21∑k(y^k−dk)2
目标:计算 ∂wji∂E。
根据链式法则:
∂wji∂E=∂xj∂E⋅∂wji∂xj
第一步:局部导数
∂wji∂xj=yi
第二步:全局误差信号
∂xj∂E=∂yj∂E⋅f′(xj)
其中:
∂yj∂E=k∑∂y^k∂E⋅∂yj∂y^k=k∑(y^k−dk)vkj
(假设输出层为线性:y^k=∑jvkjyj+ck)
因此:
∂xj∂E=[k∑(y^k−dk)vkj]⋅f′(xj)
最终梯度:
∂wji∂E=[k∑(y^k−dk)vkj]⋅f′(xj)⋅yi
4.3 误差向前层传递
为支持更深网络,需将误差继续向前传递:
∂yi∂E=j∑∂xj∂E⋅wji
该式表明:前一层神经元的误差信号是其所有下游神经元误差的加权和。
总结
神经网络的学习能力源于其非线性表达能力与端到端参数优化机制的结合。单个神经元本质上是带偏置的线性变换,但通过堆叠多层并引入可导的激活函数(如 ReLU、Sigmoid、Tanh),网络能够将输入映射到高维非线性空间,从而解决线性不可分问题。这种结构即为多层感知机(MLP),是现代深度学习模型的理论基石。
训练过程依赖两个核心流程:
- 前向传播完成从输入到预测的计算,并通过 Softmax 等输出层生成概率分布;
- 反向传播则利用链式法则,高效计算损失函数对所有参数的梯度,为优化算法(如梯度下降)提供更新依据。
其中,链式法则的逐层分解机制,使得即使面对数百万参数,梯度仍能以线性时间复杂度完成计算。这一设计不仅解决了早期感知机无法训练多层结构的瓶颈,也构成了当今所有深度学习框架(如 PyTorch、TensorFlow)自动微分系统的数学基础。