数据结构（二）

第四章：树和二叉树

一、树的定义

1. 基本概念

树（Tree） ：是 n（n ≥ 0）个结点的有限集合。当 n = 0 时称为空树。有一个特定的结点称为根结点（Root） 。其余结点可分为 m（m ≥ 0）个互不相交的有限集合，每个集合本身就是一棵树，称为根的子树（Subtree） 。

2. 基本术语

1. 结点的度：子树的个数。

2. 树的度：所有结点中最大的度。

3. 叶结点（终端结点） ：度为 0 的结点。

4. 分支结点（非终端结点） ：度不为 0 的结点。

5. 孩子、双亲、兄弟：父子关系。

6. 路径与路径长度：从一个结点到另一个结点所经过的边数。

7. 层次、深度、高度：

   • 根结点在第 1 层（或第 0 层）。
   • 结点的深度：从根到该结点的层数。
   • 树的高度：所有结点中最大深度。

二、二叉树的性质（重点）

1. 二叉树定义

每个结点最多有两个子树（左子树、右子树），且左右子树有顺序之分。

2. 五条重要性质（常考选择题、填空题）

设二叉树的深度为 h，结点总数为 n

性质	内容
性质1	第 i 层最多有 $2^{i-1}$ 个结点（i ≥ 1）
性质2	深度为 h 的二叉树最多有 $2^h - 1$ 个结点（满二叉树）
性质3	对任何二叉树，若度为 0 的结点数为 $n_0$，度为 2 的结点数为 $n_2$，则：$n_0 = n_2 + 1$
性质4	具有 n 个结点的完全二叉树的深度为：$\lfloor \log_2 n \rfloor + 1$
性质5	完全二叉树中，编号为 i 的结点： - 若 $2i \leq n$，则左孩子编号为 $2i$ - 若 $2i+1 \leq n$，则右孩子编号为 $2i+1$ - 若 $i > 1$，则双亲编号为 $\lfloor i/2 \rfloor$

三、线索化二叉树（Threaded Binary Tree）

1. 为什么需要线索化？

普通二叉树遍历依赖栈或递归，空间开销大。线索化是为了高效实现非递归遍历，利用空指针指向前驱/后继。

2. 线索化原理

• 利用空指针域：若左孩子为空，令其指向前驱；右孩子为空，指向后继。

• 增加两个标志位：

  ​ltag​：0 表示 left 指向左孩子，1 表示指向前驱

• ​rtag​：0 表示 right 指向右孩子，1 表示指向后继

3. 三种线索化

• 前序线索二叉树
• 中序线索二叉树（最常见）
• 后序线索二叉树

4. 线索化的作用

• 实现非递归、不使用栈的遍历
• 节省空间，提高效率

四、树与二叉树的转换（常考画图题）

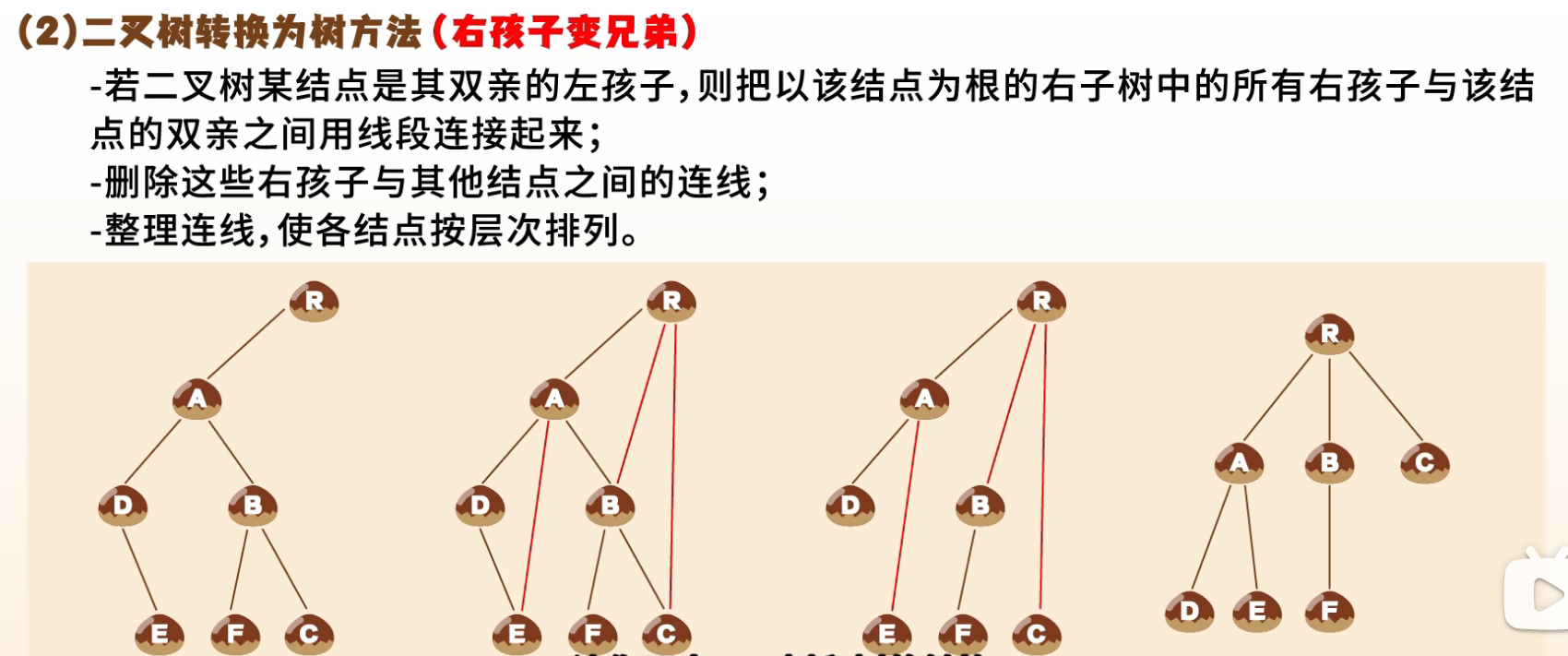
1. 树 → 二叉树（左孩子右兄弟表示法）

规则：

• 每个结点的左指针指向它的第一个孩子
• 右指针指向它的下一个兄弟

2. 森林 → 二叉树

• 将每棵树转为二叉树
• 第一棵树的根作为总根
• 后面各树的根作为前一棵树根的“右兄弟”（即挂在右子树链上）

3. 二叉树 → 树/森林

• 逆过程：右孩子视为兄弟，左孩子视为孩子
• 断开所有“右子树”连接，形成多棵树 → 森林

五、哈夫曼编码（Huffman Coding）——重点应用！

1. 哈夫曼树（最优二叉树）

• 带权路径长度（WPL）最小的二叉树
• 权值大的结点尽量靠近根

2. 构造哈夫曼树（贪心算法）

步骤：

1. 把每个权值当作一个独立的结点（叶子）
2. 选两个权值最小的结点合并，生成新结点，权值为两者之和
3. 放回集合，重复直到只剩一棵树

✅ 注意：每次选最小的两个，不排序也可以，但通常排序方便

3. 哈夫曼编码

• 从根到叶子的路径：左分支为 0，右分支为 1（或反之）
• 得到的二进制串即为该字符的编码
• 特点：前缀编码（任一编码不是另一个的前缀），可唯一解码

第六章：图

一、图的定义（基础概念）

1. 基本定义

• 图（Graph） ：由顶点集合 $V$ 和边集合 $E$ 组成，记作 $G = (V, E)$
• 顶点（Vertex） ：数据元素
• 边（Edge） ：连接两个顶点的结构

2. 分类

类型	说明
无向图	边无方向，$(u,v) = (v,u)$
有向图	边有方向，$<u,v> \neq <v,u>$
带权图（网）	每条边有数值（权重）
简单图	无自环、无重边
完全图	每对顶点之间都有边
- 无向完全图：边数 = $\frac{n(n-1)}{2}$ - 有向完全图：边数 = $n(n-1)$

3. 基本术语

• 度（Degree） ：

  无向图：一个顶点的边数；有向图：入度（指向该点） + 出度（从该点指出）

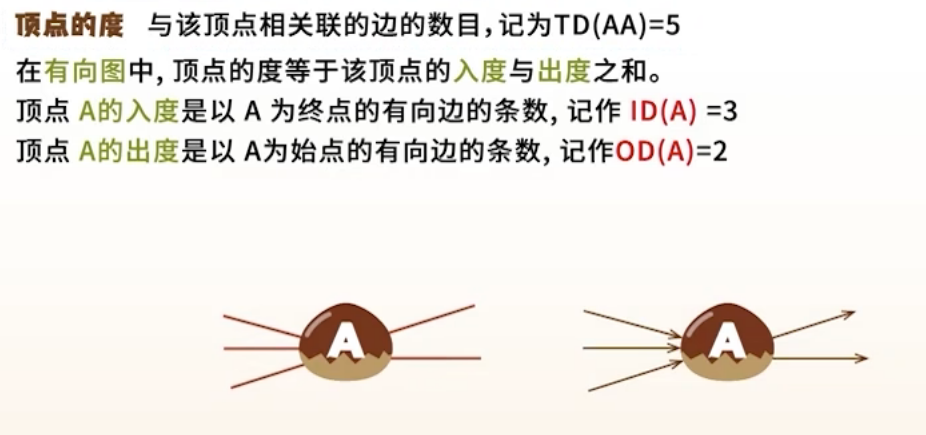
• 路径、路径长度、回路（环）

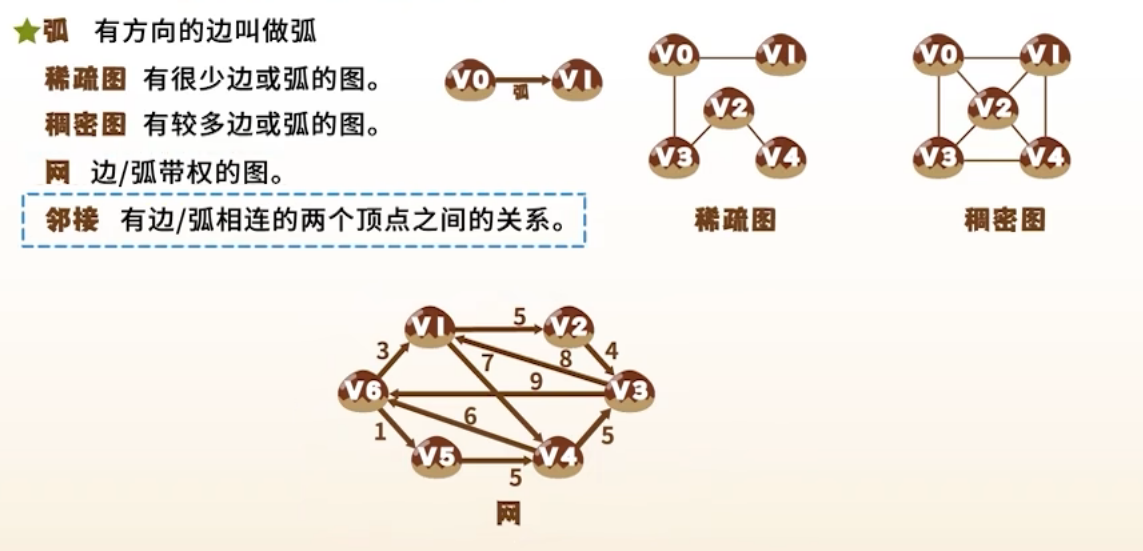
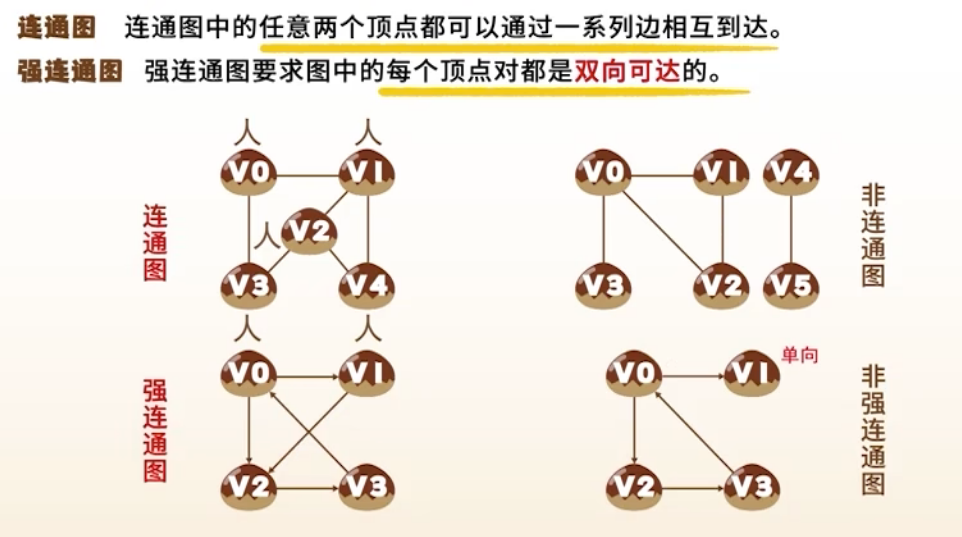
• 连通图（无向图中任意两点可达）；强连通图（有向图中任意两点互相可达）

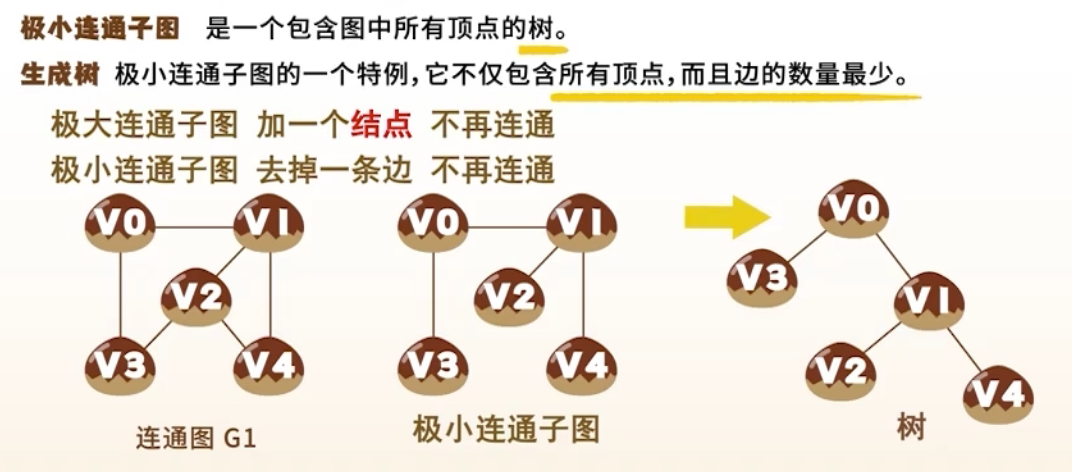
• 生成树：连通图的极小连通子图，含所有顶点，$n-1$ 条边\

​​​​​

二、图的表示法（存储结构）

1. 邻接矩阵表示法（Adjacency Matrix）

结构

• 用二维数组 $A[i][j]$ 表示边
• $A[i][j] = 1$ 表示有边（或权重），否则为 0 或 ∞

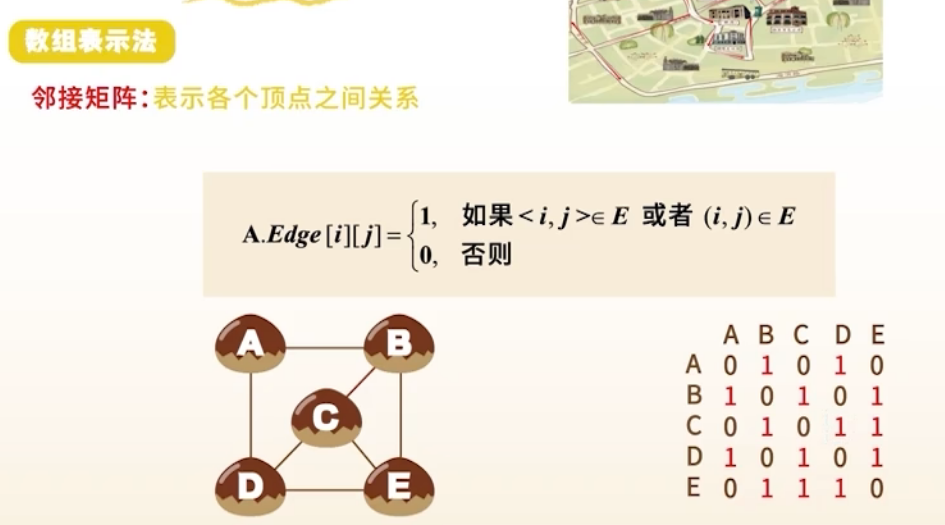
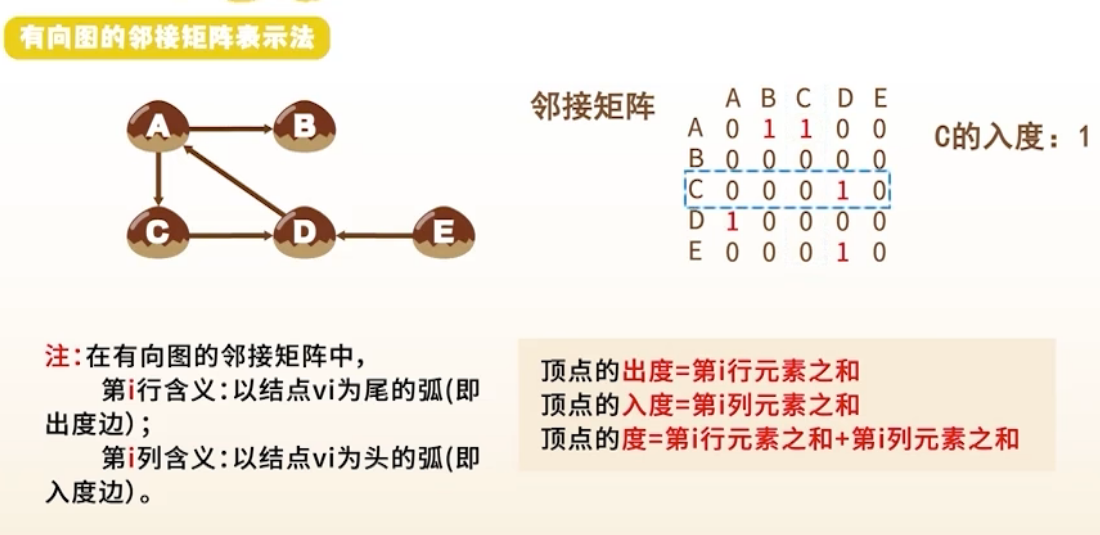
特点

优点	缺点
实现简单，适合稠密图	空间复杂度 $O(n^2)$，浪费空间（稀疏图）
判断边是否存在快 $O(1)$	添加/删除顶点代价高

2. 邻接表表示法（Adjacency List）

结构

• 每个顶点对应一个链表，存储其所有邻接点
• 带权图：链表结点包含 vertex, weight, next​

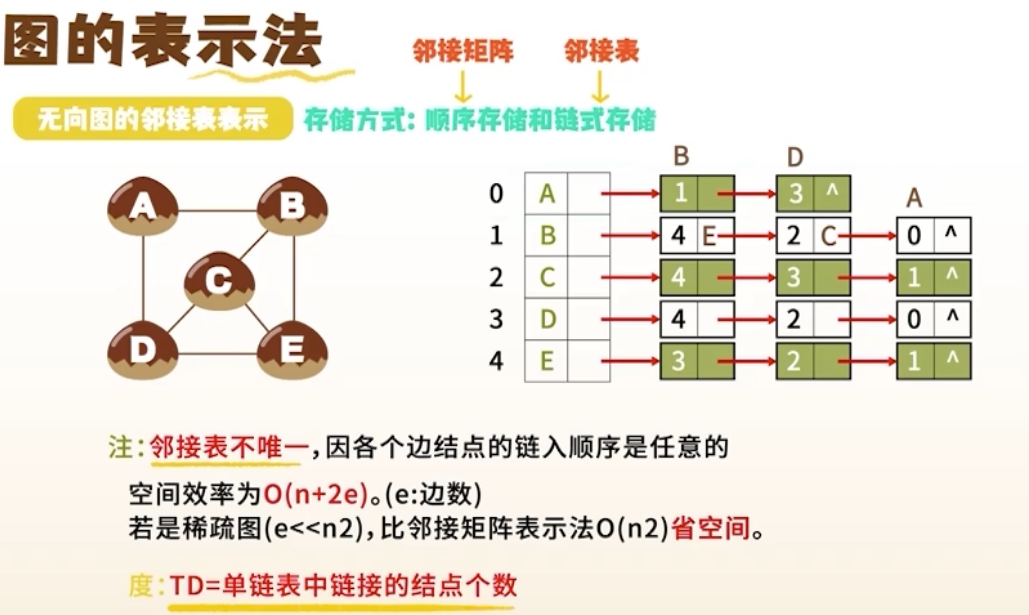
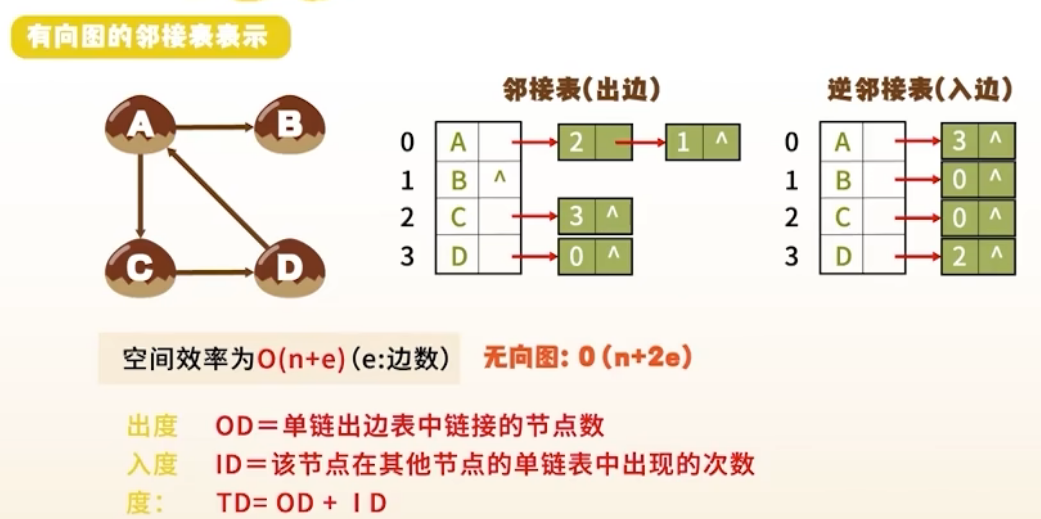
特点

优点	缺点
空间省，适合稀疏图 $O(n+e)$	判断边存在需遍历链表 $O(\text{度})$
易于遍历邻接点	实现稍复杂

三、图的遍历（核心算法）

1. 深度优先搜索（DFS, Depth-First Search）

思想

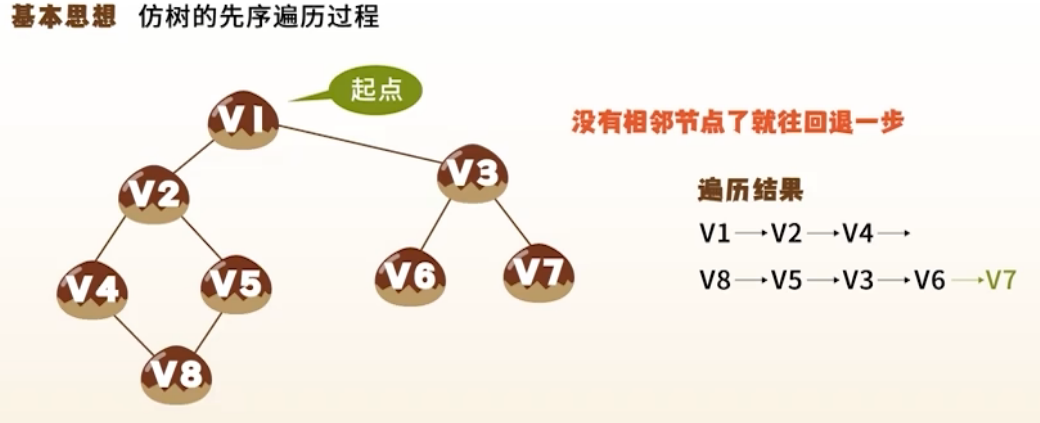
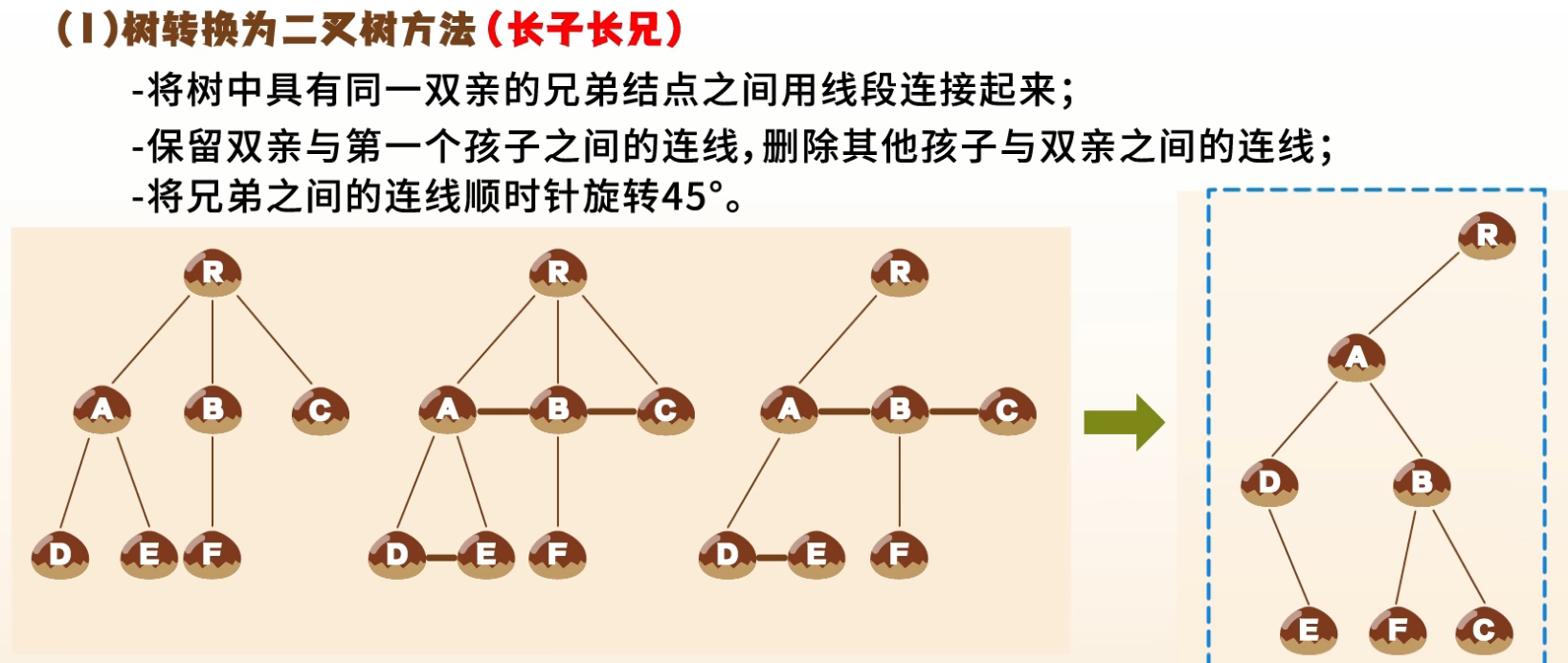
类似树的先序遍历

“一条路走到黑”，回溯再探其他路径

使用 递归 或 栈

算法步骤

1. 访问当前顶点，标记已访问
2. 找到一个未访问的邻接点，递归 DFS
3. 若无未访问邻接点，回溯

时间复杂度

• 邻接矩阵：$O(n^2)$
• 邻接表：$O(n + e)$

2. 广度优先搜索（BFS, Breadth-First Search）

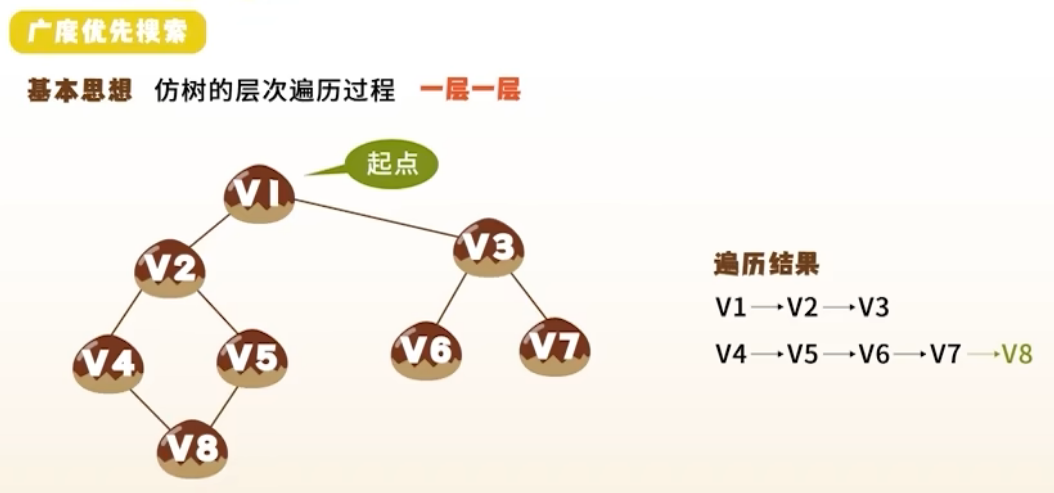
思想

• 类似树的层序遍历
• “一圈一圈往外扩”
• 使用 队列

算法步骤

1. 访问起始顶点，入队
2. 出队一个顶点，访问其所有未访问邻接点，入队
3. 重复直到队列为空

时间复杂度

邻接矩阵：$O(n^2)$

邻接表：$O(n + e)$

DFS vs BFS 对比

对比项	DFS	BFS
数据结构	栈（递归）	队列
应用	路径存在、拓扑排序	最短路径（无权图）
空间	$O(h)$（深度）	$O(w)$（宽度）
特点	深入优先	层层扩展

四、最小生成树（Minimum Spanning Tree, MST）

适用于连通无向带权图，目标：选 $n-1$ 条边，连接所有顶点，总权值最小。

1. Prim 算法（普里姆）​​

思想

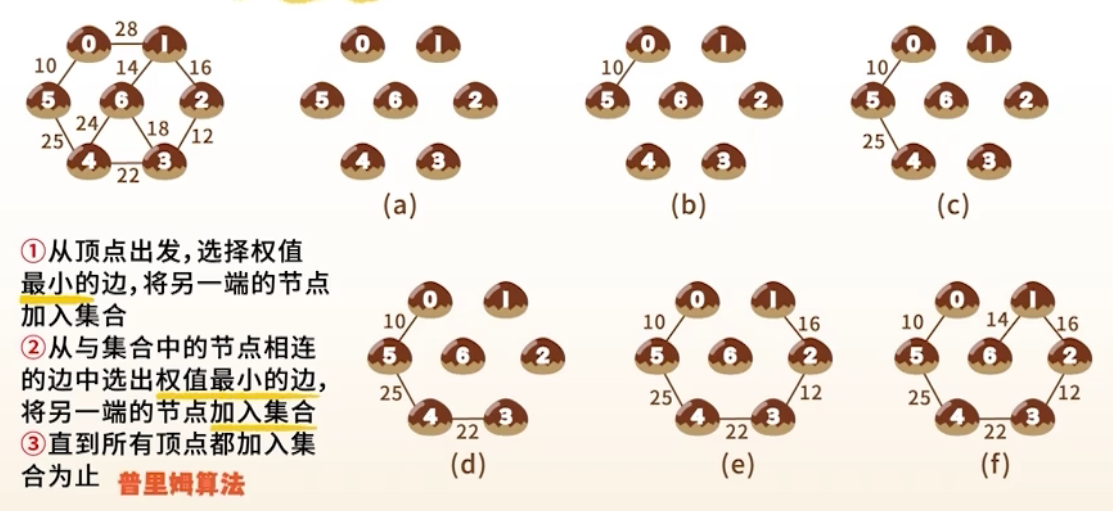
• 从点出发，逐步扩展生成树，每次选一个离当前生成树最近的顶点加入，类似 Dijkstra（贪心）

时间复杂度

邻接矩阵：$O(n^2)$

优先队列优化：$O(e \log n)$

2. Kruskal 算法（克鲁斯卡尔）

思想

从边出发，每次选权值最小且不构成环的边，使用 并查集 判断是否连通（是否成环）

时间复杂度

$O(eloge)$

Prim vs Kruskal 对比

对比项	Prim	Kruskal
出发点	顶点	边
适用图	稠密图	稀疏图
数据结构	距离数组	并查集 + 边排序
是否需连通	是（Prim 从一个点开始）	否（Kruskal 可判断是否连通）

五、最短路径（Shortest Path）

1. Dijkstra 算法（单源最短路径）

适用

• 带权图（权 ≥ 0）
• 求一个源点到其他所有顶点的最短路径

思想

• 贪心策略：每次选距离最小的未确定顶点，更新其邻接点
• 使用 dist[]​ 数组记录最短距离

时间复杂度

• 邻接矩阵：$O(n^2)$
• 优先队列优化：$O((n+e) \log n)$

步骤	当前选点	dist[0]	dist[1]	…	前驱
初始化	-	0	∞	…	-

2. Floyd 算法（多源最短路径）

适用

• 求任意两点间的最短路径
• 可处理负权边（但不能有负权环）

思想

• 动态规划：$D[k][i][j] = \min(D[k-1][i][j], D[k-1][i][k] + D[k-1][k][j])$
• 通常用二维数组滚动：dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])​

时间复杂度

$O(n^3)$

Dijkstra vs Floyd 对比

对比项	Dijkstra	Floyd
源点	单源	多源（所有点对）
时间复杂度	$O(n^2)$	$O(n^3)$
负权边	❌ 不行	✅ 可以（无负环）
实现难度	中等	简单（三重循环）

第七章：查找

一、查找的基本原理

1. 什么是查找？

• 在一个数据集合中寻找某个“特定元素”是否存在的过程。
• 查找成功：返回该元素的位置或信息
• 查找失败：返回失败标志

2. 查找表（Search Table）

• 由同一类型的数据元素（或记录）构成的集合

• 可分为：

  • 静态查找表：只查不改（如顺序、折半、分块查找）
  • 动态查找表：支持插入和删除（如二叉排序树、AVL、B树）

3. 关键字（Key）

• 用于标识数据元素的某个字段
• 主关键字：唯一标识（如学号）
• 次关键字：可重复（如姓名）

4. 平均查找长度（ASL, Average Search Length）

• 衡量查找效率的核心指标
• 定义：为确定元素位置，平均需要比较关键字的次数

公式：

$$ASL = \sum_{i=1}^{n} P_i \times C_i$$

• $P_i$：查找第 $i$ 个元素的概率
• $C_i$：找到第 $i$ 个元素所需的比较次数

二、折半查找（Binary Search）—— 仅适用于有序表

1. 基本思想

在有序顺序表中，每次取中间元素比较。若相等则成功，若目标小，则在左半区继续，若目标大，则在右半区继续

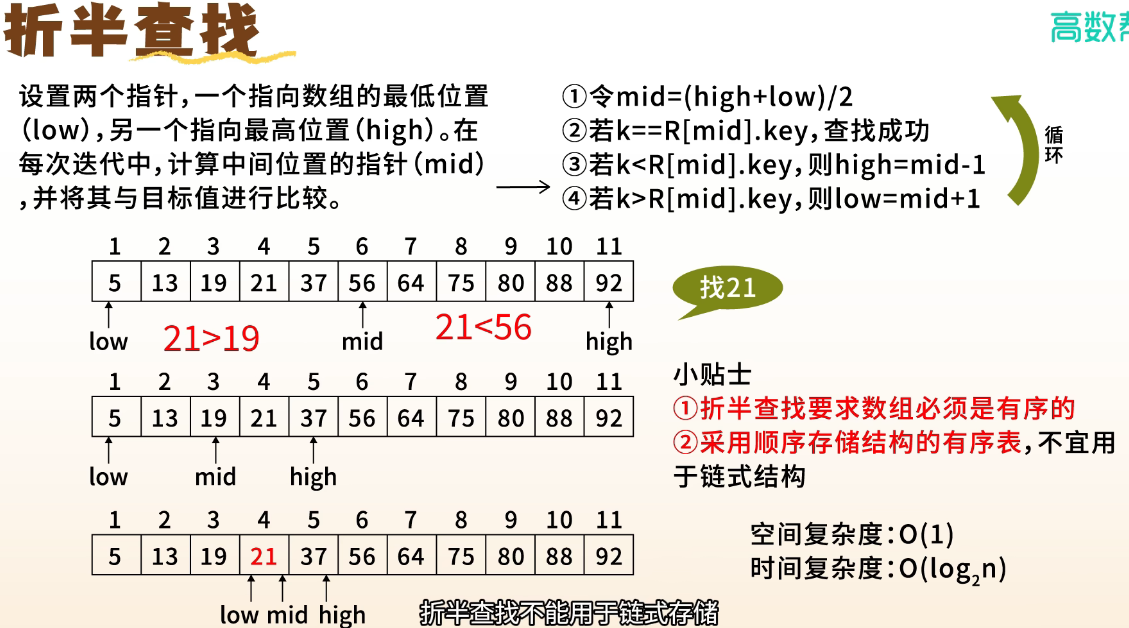
2. 实现方式

int binary_search(int arr[], int n, int key) {
    int low = 0, high = n - 1;
    while (low <= high) {
        int mid = (low + high) / 2;
        if (arr[mid] == key) return mid;
        else if (key < arr[mid]) high = mid - 1;
        else low = mid + 1;
    }
    return -1; // 未找到
}

3. 性能分析

情况	ASL 近似值
最好情况	$O(1)$（第一次就命中）
最坏情况	$O(\log_2 n)$
平均情况	$ASL \approx \log_2(n+1) - 1$

特点：

• 必须是顺序存储 + 有序表
• 不适合频繁插入/删除（维护有序代价高）

三、分块查找（Block Search / Index Sequential Search）

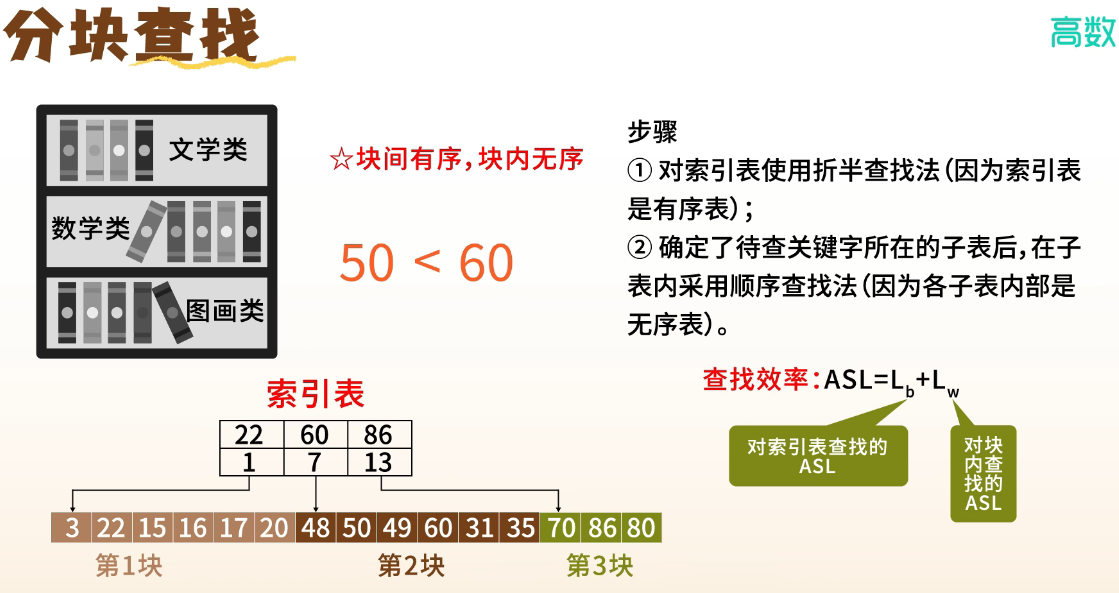
1. 基本思想（折中策略）

• 将表分为若干“块”
• 块内无序，但块间有序（即每块的最大关键字 < 下一块的最小）
• 建立一个索引表，记录每块的最大关键字和起始位置

2. 查找过程

1. 在索引表中顺序或折半查找，确定目标在哪一块
2. 在该块内进行顺序查找

3. 性能分析

• 若总长 $n$，分 $b$ 块，每块 $s$ 个元素（$s \approx n/b$）
• 索引查找 ASL ≈ $b/2$，块内查找 ASL ≈ $s/2$
• 总 ASL ≈ $\frac{b}{2} + \frac{s}{2} = \frac{s}{2} + \frac{n}{2s}$
• 最优时 $s = \sqrt{n}$，此时 $ASL \approx \sqrt{n}$

四、二叉排序树（Binary Search Tree, BST）

1. 定义

• 空树 或 满足：

  左子树非空：所有结点关键字 < 根

  右子树非空：所有结点关键字 > 根

• 左右子树也都是二叉排序树

2. 操作

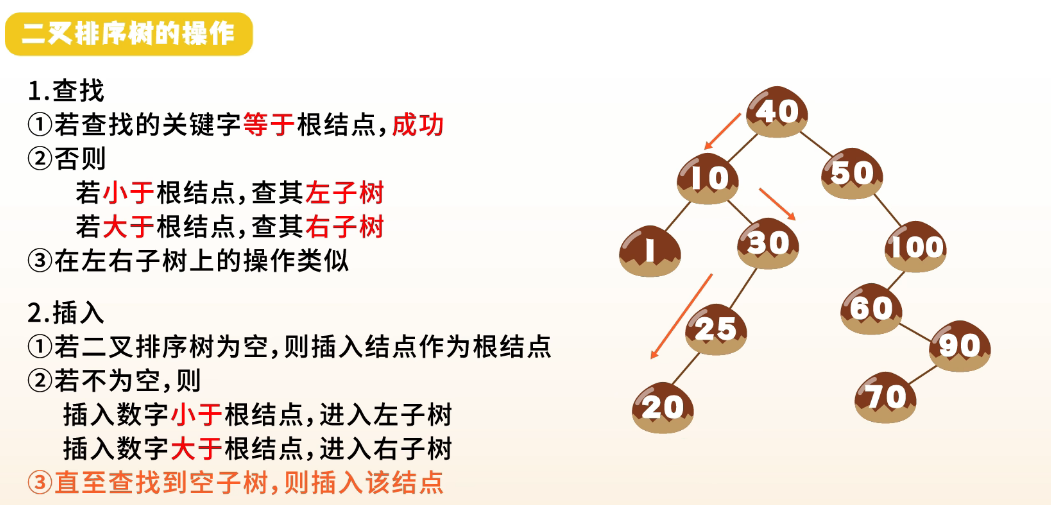
3. 性能分析

情况	时间复杂度
最好（平衡）	$O(\log n)$
最坏（退化为链）	$O(n)$

五、平衡二叉树（AVL Tree）

1. 为什么需要 AVL？

• 解决 BST 可能退化为单支树的问题

2. 定义

• 任意结点的左右子树高度差 ≤ 1
• 是一棵二叉排序树

3. 平衡因子（BF）

• $BF = h_{左} - h_{右}$，只能是 -1, 0, 1

4. 失衡与旋转

插入新结点可能导致失衡，需通过旋转恢复平衡：

失衡类型	旋转方式	口诀
LL型（左左）	右单旋	“左重右转”
RR型（右右）	左单旋	“右重左转”
LR型（左右）	先左后右双旋	“先左转再右转”
RL型（右左）	先右后左双旋	“先右转再左转”

5. 性能

• 查找、插入、删除：$O(\log n)$
• 维护平衡代价较高，适合查找频繁的场景

六、哈希表（Hash Table）—— 散列表

1. 基本思想

• 直接定址：通过关键字直接计算出存储位置
• 核心：$\text{地址} = H(key)$

2. 哈希函数构造方法

方法	说明	示例
除留余数法	$H(key) = key \mod p$（p 为不大于表长的素数）	最常用
直接定址法	$H(key) = key$ 或 $a \times key + b$	线性
数字分析法	取关键字中分布均匀的几位	多位学号
平方取中法	取 key² 的中间几位	适合未知分布

3. 冲突（Collision）

• 不同关键字得到相同哈希地址 → 冲突不可避免！

4. 处理冲突的方法

（1）开放定址法（Open Addressing）

• 一旦冲突，就找下一个空位置
• 公式：$H_i = (H(key) + d_i) \mod m$

探测方式	$d_i$ 序列	特点
线性探测	$1,2,3,...$	易“堆积”
平方探测	$1^2,-1^2,2^2,-2^2,...$	避免堆积，但可能找不到空位
伪随机探测	随机数序列	不常用

（2）链地址法（拉链法）

• 把冲突的关键字用链表串起来
• 每个哈希地址对应一个单链表

5. 哈希表查找性能

• 理想情况：$O(1)$
• 实际 ASL 与装填因子 α = n/m 有关（n：元素数，m：表长）
• α 越小，冲突越少，但空间利用率低
• 一般建议 α ≤ 0.7～0.8

七、各查找方法对比总结

查找方法	适用结构	时间复杂度（平均）	是否动态	备注
顺序查找	顺序/链式	$O(n)$	✅	最简单
折半查找	有序顺序表	$O(\log n)$	❌	静态为主
分块查找	顺序存储	$O(\sqrt{n})$	✅	折中方案
二叉排序树	链式	$O(\log n)$（最好）	✅	易退化
AVL树	链式	$O(\log n)$	✅	严格平衡
哈希表	顺序/链式	$O(1)$	✅	冲突处理关键

第八章：排序

一、排序的基本概念

1. 什么是排序？

• 将一组无序的记录序列重新排列成按关键字递增或递减的有序序列。
• 输入：n 个记录 $R_1, R_2, ..., R_n$，关键字为 $k_1, k_2, ..., k_n$
• 输出：重排后使得 $k_{i1} \leq k_{i2} \leq ... \leq k_{in}$

2. 内部排序 vs 外部排序

类型	特点
内部排序	数据全部在内存中完成排序（本章重点）
外部排序	数据量太大，需借助外存（如归并排序的外排版本）

3. 排序的评价指标

指标	说明
时间复杂度	比较和移动次数，影响运行效率
空间复杂度	额外内存使用量
稳定性	相同关键字的记录，排序后相对位置不变
适用场景	数据规模、初始状态（如是否基本有序）

二、五大类排序算法详解

1. 插入排序（Insertion Sort）

（1）直接插入排序（Straight Insertion Sort）

思想：

• 将每个元素插入到已排序部分的正确位置
• 类似打扑克牌时理牌

步骤：

1. 第一个元素视为已排序
2. 从第二个开始，依次与前面已排序部分从后往前比较
3. 找到合适位置插入（后移元素腾位置）

算法实现：

对比折半插入排序

性能分析：

情况	时间复杂度	说明
最好（已有序）	$O(n)$	只比较不移动
最坏（逆序）	$O(n^2)$	每次都要前移
平均	$O(n^2)$	——
空间复杂度	$O(1)$	原地排序
稳定性	稳定	相同元素不会跨过

（2）希尔排序（Shell Sort）——插入排序的改进

思想：

• 分组进行直接插入排序
• 初始增量大，逐步缩小增量（最后一趟增量为1）

例子：序列 [9,8,7,6,5,4,3,2,1]​，增量序列 4→2→1​

性能分析：

情况	时间复杂度	说明
平均	$O(n^{1.3})$ 左右	依赖增量序列
最坏	$O(n^2)$	如增量选择不好
空间复杂度	$O(1)$	——
稳定性	❌ 不稳定	分组可能导致相同元素相对位置改变

2. 交换排序（Exchange Sort）

（1）冒泡排序（Bubble Sort）

思想：

• 两两比较相邻元素，逆序则交换
• 每趟将最大（或最小）元素“浮”到末尾

优化：若某趟没有发生交换 → 已有序 → 提前结束

算法实现：

性能分析：

情况	时间复杂度
最好（有序）	$O(n)$（带优化）
最坏/平均	$O(n^2)$
空间复杂度	$O(1)$
稳定性	✅ 稳定

（2）快速排序（Quick Sort）——重点中的重点！

思想（分治法） ：

1. 选一个基准（pivot）
2. 将数组分为两部分：左边 ≤ pivot，右边 ≥ pivot（一次划分 partition）
3. 递归对左右子数组排序

划分方法（常用前后指针法） ：

• 以第一个元素为 pivot
• 用 i​ 和 j​ 从两端向中间扫描，交换逆序对
• 最后将 pivot 放到中间正确位置

性能分析：

情况	时间复杂度	说明
最好（每次均分）	$O(n \log n)$	递归深度 $\log n$
最坏（已有序，pivot 极端）	$O(n^2)$	退化为冒泡
平均	$O(n \log n)$	实际表现优秀
空间复杂度	$O(\log n)$	递归栈深度
稳定性	❌ 不稳定	相同元素可能被交换跨过

3. 选择排序（Selection Sort）

（1）简单选择排序（Simple Selection Sort）

思想：

• 每趟从未排序部分选出最小（或最大）元素
• 与未排序部分的第一个元素交换

步骤：

[64, 25, 12, 22, 11]  
→ 找最小11，与64交换 → [11, 25, 12, 22, 64]  
→ 找最小12，与25交换 → [11, 12, 25, 22, 64]  
→ ...

算法实现：

性能分析：

情况	时间复杂度	说明
所有情况	$O(n^2)$	每次都要遍历找最小
空间复杂度	$O(1)$	原地排序
稳定性	❌ 不稳定	交换可能破坏相对顺序（如两个12）

（2）堆排序（Heap Sort）——选择排序的改进

思想：

• 利用堆（完全二叉树）的性质：根是最大（或最小）
• 构建大根堆 → 取堆顶（最大）→ 与末尾交换 → 调整堆 → 重复

关键操作：

• 建堆：从最后一个非叶子结点开始向下调整
• 堆调整（shift_down） ：维护堆性质

性能分析：

情况	时间复杂度
所有情况	$O(n \log n)$
空间复杂度	$O(1)$
稳定性	❌ 不稳定

4. 归并排序（Merge Sort）——稳定且高效

思想（分治 + 合并） ：

1. 将数组分成两半，递归排序
2. 将两个有序子数组合并成一个有序数组

合并过程（双指针法） ：

• 用临时数组存放结果
• 比较两数组当前元素，小的放入结果

性能分析：

情况	时间复杂度
所有情况	$O(n \log n)$
空间复杂度	$O(n)$
稳定性	✅ 稳定

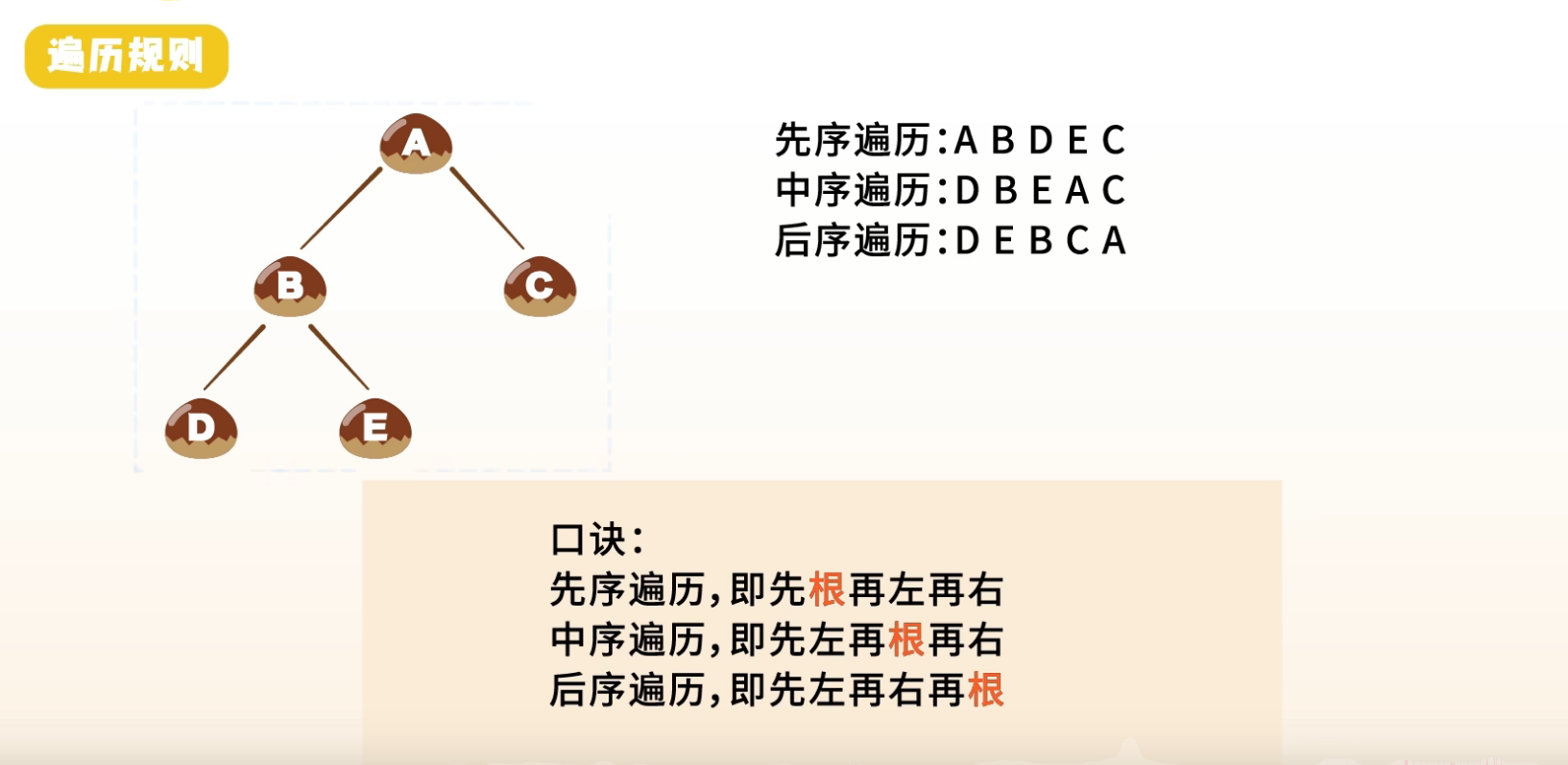
三、五大排序方法对比表

‍