周学习总结（4月6日-12日）

一、拓扑数据分析：持续同调

我对拓扑数据分析的步骤理解为：

1. 对原始数据进行数据处理，去除噪声、填补缺失值，并进行归一化处理，确保数据质量，生成点云。
2. 持续同调：通过 Vietoris-Rips（VR）复形 或 Cech复形，逐步增加半径参数ε，生成嵌套的单纯复形序列，捕捉不同尺度下的拓扑特征，并计算同调群。
3. 生成持续图，提取拓扑特征。

Morse函数

在光滑的m-maniflod$M$上的光滑函数$f : M→ \mathbb{R}$，$p$为$f$的非退化点，在$ p$邻域上有函数$U (p) $存在以$p$为原点的$m$维坐标系，使得:

$$f (x) = f (p)-x_1^2-…-x_s^2+x^2_{s+1}…+x_m^2$$

负号个数即为非退化临界点$p$的index。从而Morse函数为满足一下条件的光滑函数：

1. 所有临界点非退化
2. 所有临界点都不同

它通过一个光滑函数的临界点（即梯度为零的点：最大值、最小值点）来揭示形状的拓扑结构 。

示例图如下：

​

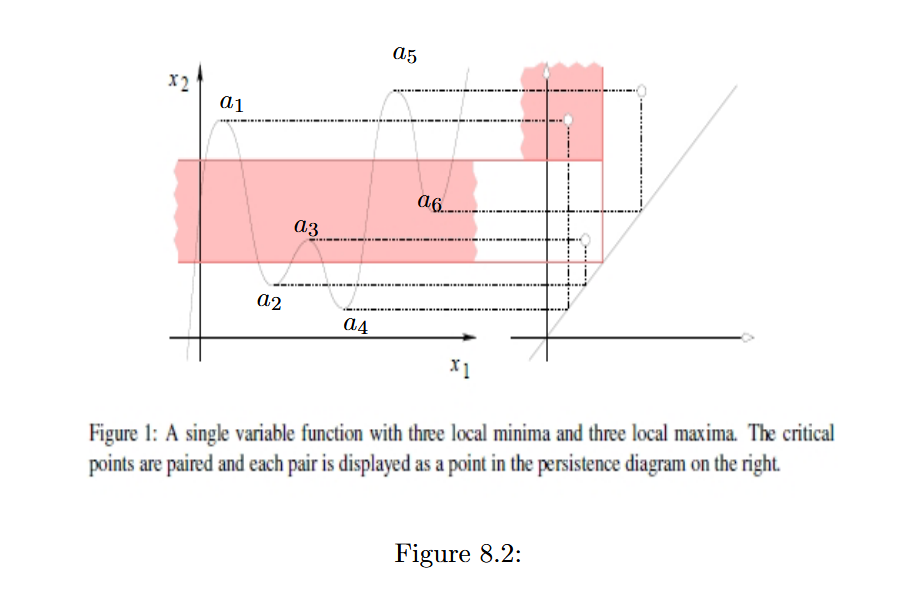
图中，$t$从$x$轴持续上升，从$f (a_4)$越过$f (a_2)$和$f(a_3)$，$f (a_2)$、$f(a_3)$结合成对，且$f (a_2)$，$f(a_3)$被消灭拉直，以此为例，剩余组合为$f (a_5)$、$f(a_6)$和$f (a_1)$、$f(a_4)$，Morse函数对应画出持续图，将组合以$y_{最小值}$为$X$轴，以$y_{最大值}$为$Y$轴，画点得到持续图。

二、C++

本周主要学习的是内容是：日期问题。

核心是使用Nextday函数：

void NextDay(int& year, int& month, int& day) {
	// & 出现在定义or形参中，表示引用，出现在其他位置表现为取缔值
	int dayOfMonth[] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 };
	int isLeap;
	isLeap = year % 400 == 0 || year % 4 == 0 && year % 100 != 0;
	if (isLeap) {
		dayOfMonth[2] = 29;
	}
	else {
		dayOfMonth[2] = 28;
	}// & 闰年判断

	++day;
	if (day > dayOfMonth[month]) {
		day = 1;
		++month;
	}
	if (month > 12) {
		month = 1;
		++year;
	}
}

​NextDay​ 函数的作用是将输入的日期（年、月、日）推进到下一天，同时处理闰年、月份切换和年份切换。

其余的根据题目要求，进行对nextday函数进行循环调用，将日期逐日推进，最后打印结果即可。

三、概率论

本周学习的是从贝叶斯定律到概率质量函数和概率密度函数。

1. 贝叶斯定律

贝叶斯定律是描述条件概率关系的公式。它的基本公式是：

$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

其中，如果存在$k$个分区，$P（A）$可以明确的以总概率形式写出：

$$P(A_i|B)=\frac{P(B|A_i)P(A_i)}{\sum_{i=0}{P(B|A_i)P(A_i)}}$$

其中：

• $P(A|B)$ 是在已知事件B发生的情况下，事件A发生的概率（后验概率）。
• $P(B|A)$ 是在事件A发生的情况下，事件B发生的概率（似然性）。
• $P(A)$ 是事件A发生的先验概率，即在没有任何条件下对事件A发生的估计。
• $P(B)$ 是事件B发生的总概率。

举个例子：假设你有一个学校考试的成绩（B），你知道大部分学生通过考试的概率是80%（$P(B)$）。但是，如果一个学生非常努力学习（事件A），那他通过考试的概率可能是90%（$P(B|A)$）。贝叶斯定律告诉你，如果你知道某个学生努力学习的概率（$P(A )$），那么你可以更准确地判断他在通过了这次考试情况下，有努力学习的概率（$P(A|B)$）。通过贝叶斯定律，我们可以计算出在通过考试的学生中，有多少人是努力学习的。

2. 概率质量函数（PMF）和概率密度函数（PDF）

概率质量函数是用来描述离散型随机变量（也就是那些可能取有限个或可数个数值的随机变量），它给出了每个特定结果发生的概率。

概率密度函数是用来描述连续型随机变量（可以取无数个数值的变量），它描述了某个区间内的概率，通过计算区域下的面积来得出概率。

简而言之：概率质量函数是用来回答独立结果发生的概率，结果与结果之间是离散、无关的。概率密度函数是计算某一个范围内的结果出现的可能性，例如：温度不是只有几个固定的数字，而是可能是任何一个数字，比如 20°C、20.1°C、20.5°C，甚至是 19.99999°C。计算温度在 20°C 到 21°C 之间的概率，就可以通过计算这个范围内的面积来得到。