训练的常见问题与解决方法

模型架构设计

模型架构决定了神经网络能“看见”什么。全连接层通用于一般函数，卷积层擅长捕捉空间局部性，循环结构理解时序，注意力则聚焦长程依赖——选择哪种结构，本质上是在回答：“这个问题的规律藏在哪里？”

很多人误以为“越大越深就越好”，但真正的挑战不在于模型能否表示复杂函数，而在于它能否从有限数据中学会这种表示。万能近似定理告诉我们：一个足够宽的单层网络理论上能逼近任何连续函数。可“足够宽”往往意味着不切实际的参数量，且优化算法未必能找到正确的解。

于是，深度学习转向了“深度”：用多层结构逐级抽象——从像素到边缘，从边缘到部件，从部件到语义。这不是为了堆砌复杂度，而是模拟人类认知的层次性。ResNet 能训练上千层，不是因为“深=强”，而是因为它让深变得​可学。

最终，好的架构不是最复杂的，而是​最契合问题本质的。它既要有足够的表达力去捕捉规律，又要有足够的克制避免陷入噪声。模型设计，是一场在能力与简约之间的哲学平衡。

模型架构决定了网络能学到什么。主要包括：

• 网络结构（层数、连接方式）
• 每层的节点数量
• 层的类型（全连接、卷积、RNN、注意力等）

设计没有固定公式，必须结合任务类型（图像、文本、时序等）和数据特点反复调整。

问题一：过拟合与欠拟合

表现

过拟合和欠拟合是深度学习训练中最典型的两类问题，本质上反映了模型能力与数据复杂度之间的失衡。无论架构多么精巧，训练过程最终会遭遇两个根本性挑战：欠拟合与​过拟合。它们本质是模型容量与数据复杂度之间的失衡。

欠拟合发生在模型能力不足时：训练误差和测试误差都很高，表明模型连训练数据中的基本模式都无法捕捉。典型例子是用线性模型拟合非线性关系，或网络太浅、参数太少。

过拟合则出现在模型过于强大时：训练误差极低，但测试误差显著升高。模型不仅学到了数据中的规律，还记住了噪声、异常值甚至采样偏差，导致泛化失败。

要有效应对这些问题，需从数据、模型和训练策略三个维度系统入手。具体方法从数据、模型、训练策略三个维度入手

解决方向

数据侧：

1. 合理选择数据集规模：小数据集容易导致过拟合，因为模型容易“背下”所有样本；适当增加数据量可提升泛化能力，但数据过大也会带来训练效率下降，需权衡。

2. 应用数据增强：尤其在图像任务中，通过对原始样本进行旋转、翻转、裁剪、加噪等变换，可低成本生成大量多样化的训练样本。这不仅缓解了数据不足引起的过拟合，还迫使模型学习更鲁棒的特征，提升在真实场景中的表现。

3. 引入验证集机制：将原始数据划分为训练集（用于学习）、验证集（用于调参和监控）和测试集（用于最终评估）。验证集相当于“模拟考试”，能在训练过程中及时发现过拟合或欠拟合趋势，避免等到训练结束才暴露问题。

模型侧：

1. 欠拟合通常通过增加模型复杂度来解决，例如增加隐藏层数、扩大每层神经元数量，或使用更强的非线性激活函数。
2. 过拟合则需谨慎控制模型容量，复杂模型（如深层网络）虽然表达能力强，但也更容易拟合噪声。因此，应遵循奥卡姆剃刀原则——在多个能达到相近性能的模型中，优先选择结构最简单的，以提升泛化能力和可解释性。

训练策略侧：

即使数据和模型固定，训练方式也能显著影响泛化：

1. 采用k折交叉验证：将训练集均分为k份，轮流用其中1份作验证集、其余k−1份训练模型，重复k次后取平均验证性能。这种方法能更稳定地评估超参数（如学习率、正则化强度）的效果，特别适用于数据量有限的场景。
2. 实施提前终止（Early Stopping） ：在训练过程中持续监控验证误差，一旦发现其连续若干轮不再下降甚至开始上升，就立即停止训练。这相当于在模型开始过拟合的拐点处“踩刹车”，既能避免资源浪费，又能获得泛化性能更优的模型。

欠拟合主要靠增强模型能力来解决，而过拟合则需要综合施策：扩充或增强数据、简化模型结构、引入验证机制并动态控制训练过程。最终目标不是让模型在训练集上表现完美，而是在未知数据上稳健可靠。

问题二：模型复杂度、泛化误差

模型的泛化能力并非随复杂度无限提升。随着模型容量（如层数、参数量）增加，训练误差持续下降，但泛化误差（测试误差）通常先降低后升高，形成一个 U 型曲线。曲线左侧是欠拟合区（模型太弱，无法捕捉数据规律），右侧是过拟合区（模型太强，记住了噪声和细节）。我们的目标不是最小化训练误差，而是找到使泛化误差最低的最优复杂度点。

为了主动控制复杂度、将模型推向该最优区域，正则化是核心手段。它通过对学习过程施加约束，牺牲一点训练拟合能力，换取更强的泛化性能。

正则化

正则化分为广义和狭义两类：广义包括数据增强、提前终止、Dropout 等；狭义主要指在损失函数中加入参数惩罚项，如 L1 和 L2 正则。

L2 正则化（权重衰减）
L2 正则化通过在原始损失函数上增加一个参数平方和的惩罚项实现：

$$\mathcal{L}_{\text{total}} = \mathcal{L}_{\text{data}} + \lambda \sum_{i} w_i^2$$

其作用是抑制权重幅值过大，使模型输出更平滑，从而提升泛化能力。从几何视角看，若原始损失的等高线为抛物面，L2 正则项的等高线在二维中是圆形、高维中是球面，最优解落在两者交点处，通常对应一组较小但非零的权重。由于优化性质良好、梯度连续，L2 是深度学习中最常用、最稳定的正则形式。

L1 正则化
L1 正则化引入的是参数绝对值之和的惩罚：

$$\mathcal{L}_{\text{total}} = \mathcal{L}_{\text{data}} + \lambda \sum_{i} |w_i|$$

与 L2 不同，L1 倾向于将不重要的权重压缩至精确为零，从而实现参数稀疏化，相当于自动进行特征选择。其几何解释是：L1 正则项的等高线在二维中为菱形、高维中为超立方体，其“尖角”更容易与损失函数等高线在坐标轴上相交，导致某些维度的权重为零。因此，L1 特别适用于高维稀疏输入或需要模型可解释性的场景。

L1 和 L2 是 $p$-范数（$\|w\|_p$）在 $p=1$ 和 $p=2$ 时的特例。正则项的一般形式为 $\lambda \|w\|_p^p$，其中超参数 $\lambda$ 控制正则强度：$\lambda$ 越大，模型越简单，但过大会导致欠拟合；$\lambda$ 过小则正则效果微弱，难以抑制过拟合，需结合验证集进行调优。需要注意的是，没有一种正则方法在所有任务上都最优——L2 更稳定，适合通用场景；L1 适合高维稀疏或需解释性的任务；两者也可结合（如 Elastic Net）。

Dropout：一种结构化的正则化方法

Dropout 是一种在训练过程中随机“关闭”部分神经元的正则化技术，由 Hinton 等人在 2012 年提出。它不修改损失函数，而是直接干预网络的前向传播路径，通过引入结构层面的随机性，防止模型对特定神经元或特征组合产生过度依赖，从而有效缓解过拟合。

工作原理与实现机制

Dropout 的核心操作是在每次训练迭代中，以预设的保留概率 $p$（如 0.5）独立地对每个神经元的输出进行“屏蔽”：以概率 $1 - p$ 将其置为 0，否则保留原值。这等价于将激活值乘以一个由 0 和 1 构成的随机掩码（mask）。值得注意的是，这种“删除”仅发生在训练阶段；在测试或推理阶段，必须使用完整的网络结构。

为了保证训练与测试阶段的输出期望一致，实践中通常采用以下两种等效策略之一：

• 训练时缩放（Inverted Dropout） ：保留的神经元输出除以 $p$，即 output = (mask * x) / p。这是目前主流框架（如 PyTorch、TensorFlow）的默认实现方式，优点是测试时无需任何修改。
• 测试时缩放：训练时不缩放，测试时将所有权重乘以 $p$。

直观理解：隐式的模型集成

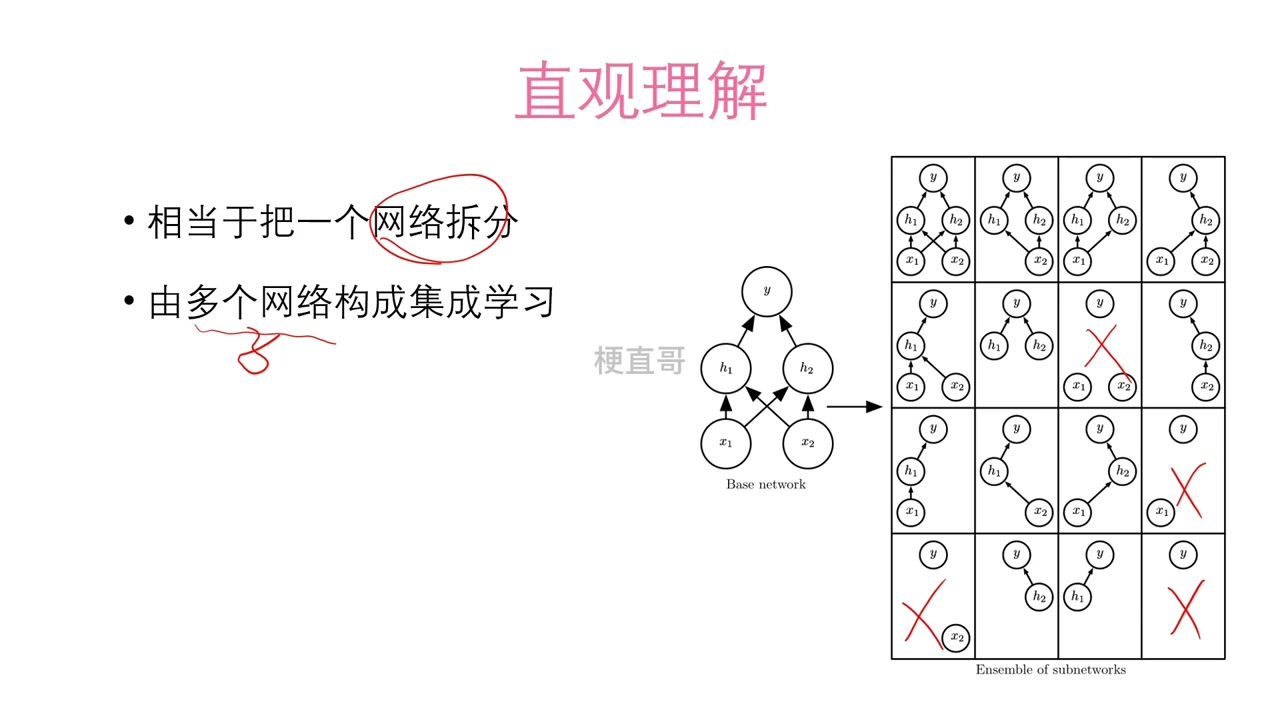
从集成学习的视角看，Dropout 相当于在每次前向传播时随机采样一个子网络进行训练。对于一个含 $n$ 个神经元的层，理论上可生成 $2^n$ 种不同的子结构。这些子网络共享同一组参数，但因随机掩码不同而表现出不同的功能。整个训练过程等价于并行训练大量弱相关的子模型，最终的模型行为可视为它们的“期望集成”，从而显著降低预测方差，提升泛化能力。

为什么 Dropout 能减少过拟合？

Dropout 通过以下机制提升模型鲁棒性：

• 打破共适应（Co-adaptation） ：神经元无法依赖其他特定神经元的存在，被迫学习更具通用性的特征表示；
• 集成效应：多个子网络的预测在期望上相互抵消个体偏差，类似于 Bagging；
• 结构正则化：与 L1/L2 正则化作用于参数值不同，Dropout 作用于网络连接结构本身，是一种动态、隐式的复杂度控制手段。

典型使用方式与代码实现

在实践中，Dropout 主要应用于全连接层，常见保留概率为：

• $p = 0.5$：标准配置，适用于中等或大型网络；
• $p = 0.3$ 或更低：用于较小网络或过拟合严重场景。

例如，一个包含 1000 个神经元的全连接层，在 $p=0.5$ 时，每次前向传播平均有 500 个神经元被激活，其余被置零。现代深度学习框架已内置 Dropout 层，无需手动实现掩码，但理解其底层逻辑有助于调试：

# 手动实现（训练阶段，Inverted Dropout）
mask = (torch.rand_like(x) < p).float()  # 生成 0/1 掩码
x = x * mask / p  # 保留的神经元缩放，保持期望不变

# 或直接使用 PyTorch 内置层
dropout = torch.nn.Dropout(p=0.5)
x = dropout(x)  # 自动处理训练/测试模式

Dropout方法打破共适应，使得神经元无法依赖其他特定神经元的存在，被迫学习更通用、更鲁棒的特征表示，通过多个子网络的预测结果在期望上相互抵消个体偏差，降低方差。与 L1/L2 不同，Dropout 作用于网络连接结构本身，是一种“隐式”的正则形式，其效果类似于对模型复杂度施加动态约束。

问题三：梯度消失与梯度爆炸

深度带来表达力，也带来脆弱性。在深层网络的训练中，梯度消失与梯度爆炸是两个如影随形的问题——它们并非实现缺陷，而是反向传播机制与深度结构结合后必然出现的数学现象。

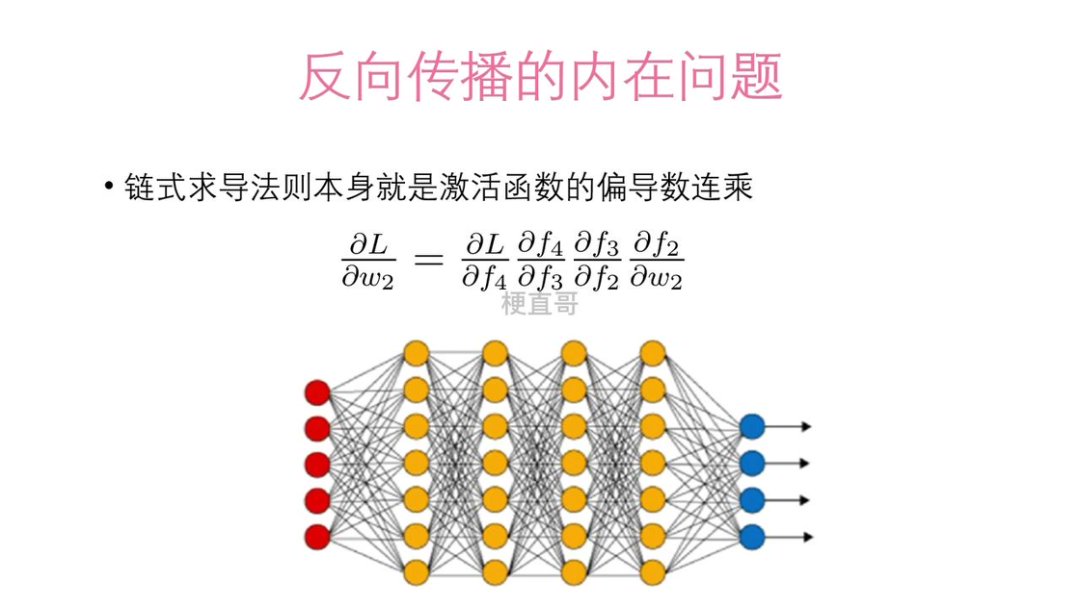
其根源在于链式法则的连乘效应。每一层的梯度由后续层的偏导数连乘而来。若每层激活函数的导数普遍小于 1（如 Sigmoid 最大导数仅 0.25），经过数十层传递后，梯度会指数级衰减至接近零，参数几乎无法更新——这就是梯度消失。反之，若权重初始化过大或某些层导数大于 1，连乘会使梯度指数增长，导致参数更新剧烈震荡，损失值爆炸甚至出现 NaN——即梯度爆炸。

这揭示了一个深刻的矛盾：网络越深，信息越难从前向后（梯度）或从后向前（信号）有效传递。Sigmoid 和 Tanh 虽具备非线性，却因其导数特性天然抑制梯度流动；而“大权重”看似增强表达，实则加剧数值不稳定性。

现代深度学习通过一系列巧妙设计化解这一困境：

ReLU 激活函数

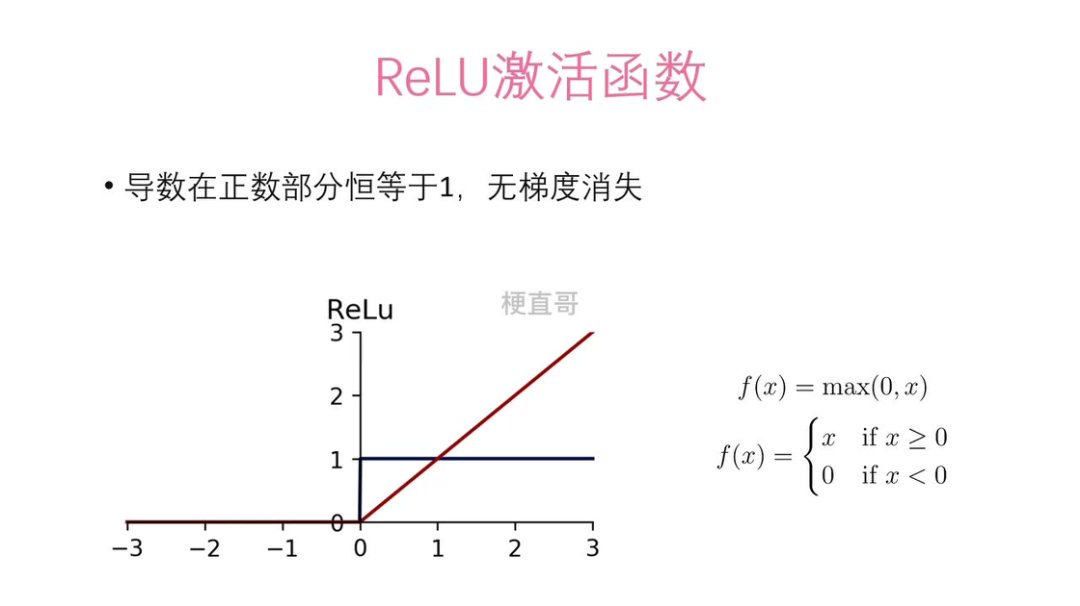
ReLU 函数在正区间导数为 1，彻底避免梯度消失，且计算效率高（无需指数运算）；但在负区间输出恒为 0，容易导致神经元“死亡”（即死亡 ReLU 问题）。为此，Leaky ReLU 等变体在负区间引入小斜率，使梯度在负区也能传递，有效缓解这一缺陷。

Batch Normalization（BN）

通过对每层输入进行标准化（均值为 0、方差为 1），将激活值约束在非饱和区域，既稳定了前向信号，也平滑了梯度分布，允许使用更大步长训练，一定程度上起到正则化作用。

残差连接（Residual Connection）

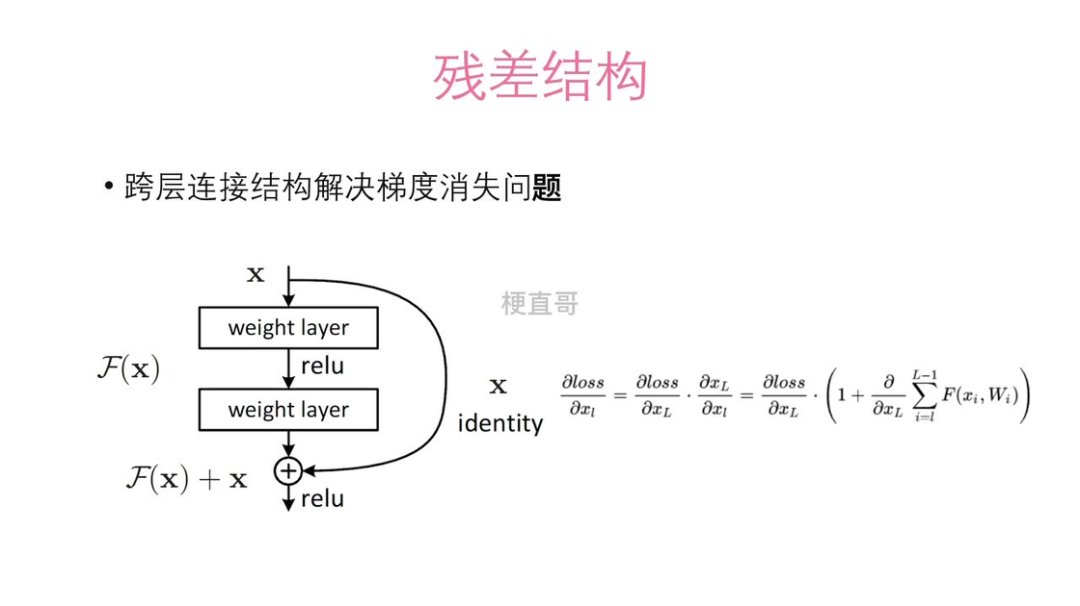
残差连接是最具突破性的解决方案。它通过跨层“捷径”（shortcut）让梯度可直接绕过非线性变换层回传，数学上保证了梯度下限。这不仅使训练上千层网络成为可能，更推动了 ResNet 在 ImageNet 上的里程碑式胜利。

梯度裁剪（Gradient Clipping）

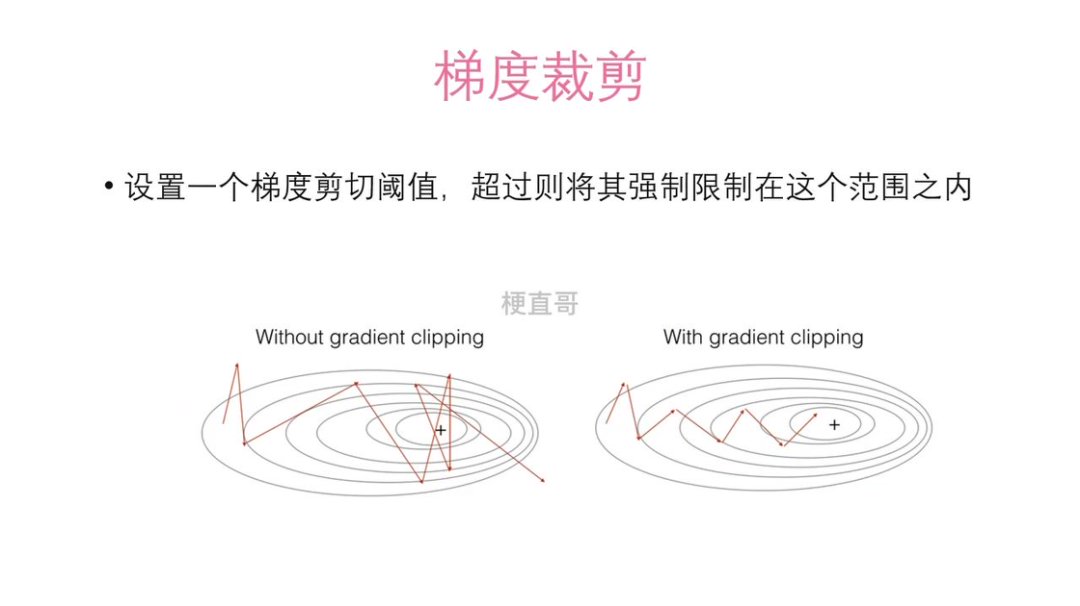
梯度裁剪是应对爆炸的“安全阀”：当梯度范数超过阈值时强制缩放，常用于 RNN 等易爆结构。

以上的这些方法往往组合使用：在工程上，神经网络通常同时采用 ReLU + BN + 残差结构，形成一套完整的梯度保护机制。真正的深度学习，不是追求层数的数字，而是确保信息能高效前传，梯度能稳定回流。

‍