梯度下降算法及其变体（下）

随机梯度下降法（SGD）：思想革命

理论基础：梯度下降的数学根基

在深度学习的训练过程中，我们面临一个核心数学问题：最小化经验风险，即在给定训练数据分布下寻找使损失函数最小的模型参数。梯度下降法（Gradient Descent）作为最基础的优化算法，通过迭代地沿着损失函数负梯度方向更新参数，成为解决这一问题的标准工具。其数学形式简洁而优雅：

$$\mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - \alpha \nabla_{\mathbf{w}} \mathcal{L}(\mathbf{w}^{(t)})$$

其中 $\mathcal{L}(\mathbf{w}) = \frac{1}{N} \sum_{i=1}^N L(\mathbf{w}; \mathbf{x}_i, y_i)$ 为经验风险，$\alpha$ 为学习率。在小规模机器学习问题中，这一方法表现优异，奠定了优化理论的基础。

范式突破：随机梯度下降的创新洞见

随机梯度下降法（SGD）通过一个看似反直觉但深刻的思想突破了这一矛盾：我们不需要完美梯度，只需一个无偏估计。SGD摒弃了全数据集梯度计算，转而采用单样本梯度：

$$\mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - \alpha^{(t)} \nabla_{\mathbf{w}} L(\mathbf{w}^{(t)}; \mathbf{x}_{i_t}, y_{i_t})$$

其中 $i_t$ 是随机采样的样本索引。这一简化带来三个革命性优势：

• 计算复杂度跃升：单次迭代复杂度从 $O(N \cdot d)$ 降至 $O(d)$，迭代频率提升数个数量级，使超大规模训练成为可能。
• 随机性转化为优势：梯度噪声不再是需要消除的干扰，而是帮助算法逃离尖锐局部极小值、收敛到泛化性能更好的平坦极小值的宝贵特性。
• 理论保证依然成立：在适当条件下，SGD能以概率1收敛到局部极小值，对非凸函数能高效逃离鞍点。

SGD的核心原理是：在随机优化中，梯度估计的无偏性比低方差更重要。在资源受限的世界里，次优但频繁的更新，往往优于完美但稀少的更新。

演进路径：超越基础SGD的优化之路

尽管SGD解决了批量梯度下降的关键瓶颈，但其自身也面临三个挑战，需要进一步优化：

• 高方差导致的震荡：单样本梯度的高方差使优化轨迹容易在最优解附近持续震荡。例如，在CIFAR-10上训练CNN时，SGD的更新方向与完整梯度方向平均夹角达60°-70°。

• 

  学习率的动态需求：固定学习率无法适应训练不同阶段的需求——初期需要大步长快速穿越高损失区域，后期需要小步长精细调整。

• 数据分布的非平稳性：在在线学习场景中，数据分布可能随时间变化，单样本梯度估计会产生系统性偏差。

为应对这些挑战，研究者提出了多种优化策略。动态学习率调整是最直接的方法：

$$\alpha^{(t)} = \frac{\alpha_0}{1 + \lambda t} \quad \text{或} \quad \alpha^{(t)} = \alpha_0 \cdot \gamma^t \quad \text{或} \quad \alpha^{(t)} = \frac{\alpha_0}{(1 + \lambda t)^2}$$

这些策略体现了"初期探索，后期精调"的优化哲学。然而，单靠调整学习率无法根本解决SGD的高方差问题。

这促使我们思考：能否在保持SGD计算效率的同时，降低梯度估计的方差？

小批量梯度下降法：工程落地的黄金标准

在深度学习的实际训练中，纯粹的随机梯度下降（SGD）虽计算高效，但其单样本梯度的高方差导致优化轨迹剧烈震荡，且无法充分利用现代硬件的并行能力。小批量梯度下降法（Mini-batch SGD）应运而生——它并非理论上的颠覆，而是一次精准的工程调和，在计算效率与梯度稳定性之间找到了最佳实践点。

梯度估计的方差-效率权衡

小批量方法的核心在于对梯度进行统计意义上的合理估计。给定批量大小 ( m )，梯度估计的方差满足：

$$\text{Var}\left[\frac{1}{m}\sum_{i=1}^{m} \nabla L(\mathbf{w}; \mathbf{x}_{i}, y_{i})\right] = \frac{\sigma^2}{m}$$

其中 ( \sigma^2 ) 是单样本梯度的方差。该公式表明：批量越大，梯度越稳定，但计算成本也越高。小批量法通过选取适中的 ( m )（通常为 32–256），在可接受的计算开销下，将梯度方差降低至单样本 SGD 的几十分之一，显著平滑了优化路径。

其更新规则为：

$$\mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - \alpha^{(t)} \cdot \frac{1}{m} \sum_{i=1}^{m} \nabla_{\mathbf{w}} L(\mathbf{w}^{(t)}; \mathbf{x}_{i_t}, y_{i_t})$$

这一定式既保留了 SGD 的迭代效率，又大幅提升了梯度的信噪比。

小批量的三大工程优势

小批量方法之所以成为现代深度学习的默认选择，源于其与硬件和系统架构的天然契合：

1. 硬件亲和性
   现代 GPU 基于 SIMD（单指令多数据）架构设计，擅长并行处理同构计算。当批量大小 ( m ) 为 32、64、128 等 2 的幂次时，内存访问对齐、线程调度效率达到峰值，实测吞吐量可比 ( m=1 ) 提升 20 倍以上。小批量不是算法妥协，而是对硬件特性的主动适配。
2. 方差与效率的最优平衡
   理论上，单位时间内的优化进展取决于“每秒有效梯度更新次数 × 梯度质量”。实验与理论均表明，当 ( m \in [32, 256] ) 时，这一乘积达到最大值——这正是小批量被广泛采用的根本原因。
3. 隐式正则化效应
   小批量引入的适度噪声并非缺陷，而是一种有益的扰动。它帮助优化器逃离尖锐的局部极小值，更倾向于收敛到平坦的极小值区域，从而提升模型泛化能力。大量实验表明，在相同训练损失下，小批量训练的模型在测试集上通常比全批量训练的模型高出 1–2% 的准确率。

固有局限：平衡背后的代价

小批量方法虽成为工程标准，但仍面临若干实践挑战：

超参数耦合敏感：批量大小 ($m$) 与学习率 ($\alpha$) 紧密耦合——增大 ($m$) 通常需同比例增大学习率（经验上按 ($\sqrt{m}$) 缩放），否则收敛变慢甚至发散；

调参空间扩大：需同时搜索 ($m \in [32, 512]$) 与 (\alpha \in [10^{{-4}, 10}{-1}])，显著增加实验成本；

资源线性增长：批量越大，GPU显存占用与计算延迟线性上升，过大 ($m$) 可能导致显存溢出或缓存效率下降。

这些局限表明，小批量并非万能解，而是在特定硬件与任务约束下的“局部最优” 。

工程现实：小批量即“标准SGD”

值得注意的是，在 PyTorch、TensorFlow 等主流框架中，当你调用SGD优化器时，默认使用的就是小批量梯度下降。这一命名惯例看似混淆，实则揭示了深度学习工程的一个基本共识：理论上的“纯SGD”（(m=1)）几乎从不用于实际训练。

小批量方法代表了一种务实的工程哲学：在资源约束下，追求“足够好且高效”的解，而非“理论上最优但不可行”的解。它不追求消除噪声，而是驾驭噪声；不追求完美梯度，而是追求高效迭代。这种在不确定性中寻找确定性的能力，正是现代 AI 系统得以扩展到亿级参数规模的关键基础。

动量法：动力学升级

理论基础：优化过程中的时间依赖性

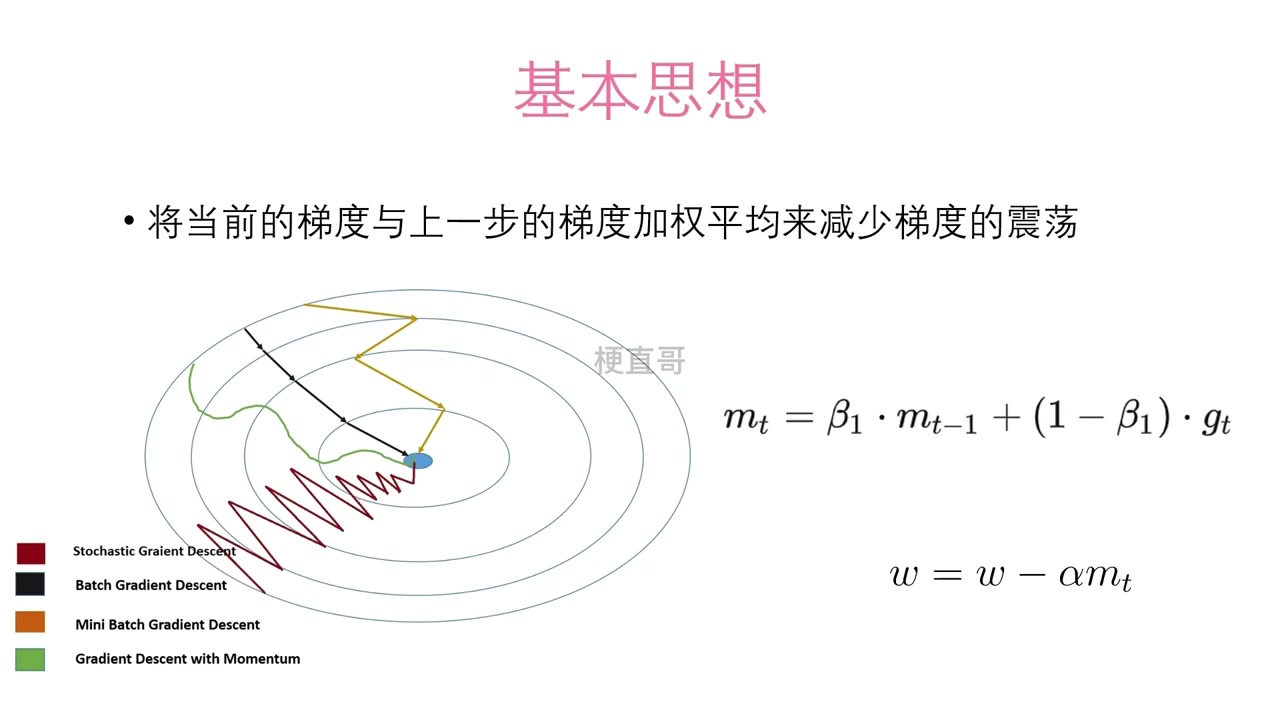
在优化理论中，标准梯度下降法假设​每次迭代的梯度信息相互独立，更新仅依赖当前梯度。然而，在深度学习的非凸优化景观中，梯度序列存在显著的时间相关性。当损失函数具有特定几何结构（如狭长山谷或鞍点区域）时，连续梯度的方向往往呈现系统性模式。

物理学为此提供了深刻隐喻：物体在力场中的运动不仅取决于瞬时受力，还受历史速度影响。动量（momentum）作为质量与速度的乘积，表征了物体维持运动状态的趋势。在优化领域，这一概念被重新诠释为：参数更新应继承历史梯度的方向信息，而非仅依赖当前快照。

一阶动量的数学形式化为历史梯度的指数加权平均：

$$\mathbf{m}_t = \beta_1 \cdot \mathbf{m}_{t-1} + (1 - \beta_1) \cdot \mathbf{g}_t$$

$$\mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - \alpha \cdot \mathbf{m}_t$$

其中 $\mathbf{g}_t = \nabla_{\mathbf{w}} L(\mathbf{w}^{(t)})$ 为当前梯度，$\beta_1 \in [0,1)$ 为动量系数（通常取0.9）。该公式本质是梯度序列的低通滤波器，抑制高频震荡，保留低频趋势。从随机过程理论看，动量法将优化轨迹从马尔可夫过程扩展为具有短期记忆的非马尔可夫过程，显著提升了在病态曲率区域的收敛效率。

范式突破：历史梯度的工程化利用

动量法通过引入历史记忆机制，从根本上重构了优化轨迹的动力学特性。其核心突破体现在三个方面：

方向惯性机制：当连续梯度指向相似方向时，动量向量 $\mathbf{m}_t$ 会累积增长，产生加速效应；当梯度方向频繁变化时，历史项相互抵消，抑制震荡。在狭长山谷中，这一机制使优化器沿谷底方向快速前进，同时抑制垂直方向的摆动。理论证明，对于二次函数 $f(\mathbf{w}) = \frac{1}{2}\mathbf{w}^\top \mathbf{H}\mathbf{w}$，动量法的收敛速度与Hessian条件数 $\kappa$ 的关系从 $O(\kappa)$ 降至 $O(\sqrt{\kappa})$。

鞍点逃逸增强：动量的惯性效应帮助优化器积累足够能量穿越鞍点。在鞍点附近，虽然当前梯度小，但历史梯度的累积可提供"推力"。分析表明，动量法将鞍点逃逸时间从指数级降至多项式级，对高维问题尤为重要。

噪声过滤能力：动量作为低通滤波器，有效抑制梯度噪声中的高频分量。当梯度噪声为零均值时，动量法的渐近方差为 $\frac{(1-\beta_1)^2}{1-\beta_1^2}\sigma^2 = \frac{1-\beta_1}{1+\beta_1}\sigma^2$，其中 $\sigma^2$ 为原始噪声方差。当 $\beta_1=0.9$ 时，方差降低至原始的5.3%，显著提升信噪比。

动量法的工程实现简洁而优雅：仅需额外存储一个与参数同维的动量向量，并增加一次向量加法。这种微小开销换来的是2-5倍的收敛加速，在ImageNet等大规模任务中可节省数千GPU小时。更重要的是，它揭示了一个优化哲学：历史信息是应对不确定性的宝贵资源。这不仅是技术改进，更是认知范式的转变——从"瞬时决策"到"基于历史的预测性优化"。

固有局限：惯性的代价

动量法虽显著加速收敛，其引入的惯性也带来新问题：

动量法需要维护与参数同维的动量向量 ( $\mathbf{m}_t$ )，在十亿级模型中增加显著内存负担。同时，在计算中：动量系数 ($\beta_1$) 与学习率 ( $\alpha$) 需精细配合——( $\beta_1$ ) 过大导致响应迟钝，过小则无法抑制噪声。在接近极小值时，历史动量可能使参数“冲过头”，需配合学习率衰减或早停策略以稳定收敛。

这些局限促使研究者进一步思考：能否让学习率也具备自适应能力，从而减轻对人工调参的依赖？

演进路径：从动量到自适应优化

动量法虽显著改进了小批量SGD，但动量法仍使用全局固定学习率，无法适应不同参数的尺度差异。在稀疏特征问题中（如NLP），某些参数极少更新，需要更大步长；而高频参数则需小步长。这一局限直接催生了AdaGrad——首个为每个参数定制学习率的算法。

动量法的历史地位独特：它既是对物理直觉的巧妙迁移，更是工程智慧的结晶。从1986年Hinton在神经网络中的初步尝试，到如今成为PyTorch和TensorFlow的默认组件，动量法证明了在复杂系统中，简单的记忆机制往往比复杂的即时计算更有效。

AdaGrad算法：为每个参数定制专属学习率

在深度学习的优化历程中，AdaGrad（Adaptive Gradient Algorithm）标志着一次关键转向：从“全局统一”的学习策略，迈向“参数自治”的差异化更新。这一转变源于对参数空间异质性的深刻洞察——当不同参数对损失函数的敏感度天差地别时，强行使用相同学习率，无异于让百米飞人与马拉松选手共用一套训练计划。

理论基础：参数异质性的数学表达

传统优化算法隐含一个危险假设：所有参数维度在几何上是“平等”的。然而在现实中，损失函数在不同方向上的曲率差异巨大。例如，在自然语言处理中，高频词（如“the”）的梯度幅值可能比低频词（如“quantum”）大几个数量级；在推荐系统中，热门商品的交互信号远强于长尾商品。若使用统一学习率，高频参数会因更新过猛而震荡，低频参数则因步长太小而几乎停滞。

AdaGrad 于 2011 年由 Duchi、Hazan 和 Singer 提出，其核心思想是：每个参数应根据其自身历史梯度动态调整学习步长。算法维护一个历史梯度平方累积向量：

$$\mathbf{V}_t = \sum_{\tau=1}^{t} \mathbf{g}_\tau^2$$

并据此执行参数更新：

$$\mathbf{w}^{(t+1)} = \mathbf{w}^{(t)} - \alpha \cdot \frac{\mathbf{g}_t}{\sqrt{\mathbf{V}_t} + \epsilon}$$

其中 $\epsilon > 0$（通常取 $10^{-8}$）用于避免除零。该公式本质上对梯度进行了二阶矩归一化：历史梯度越大，当前步长越小；反之亦然。

从几何角度看，AdaGrad 在参数空间中定义了一个自适应的度量张量 $\mathbf{G}_t = \text{diag}(\sqrt{\mathbf{V}_t})$，将标准欧氏空间转换为一个与局部曲率对齐的黎曼流形。这一变换实现了尺度不变性（scale invariance）——无论输入特征的原始量级如何（从 $10^{-3}$ 到 $10^3$），算法都能自动校准更新强度。实验表明，在未经标准化的数据上，AdaGrad 的收敛速度仅比标准化后慢 15%，而标准 SGD 则慢达 300%。

范式突破：稀疏性与尺度不变的工程价值

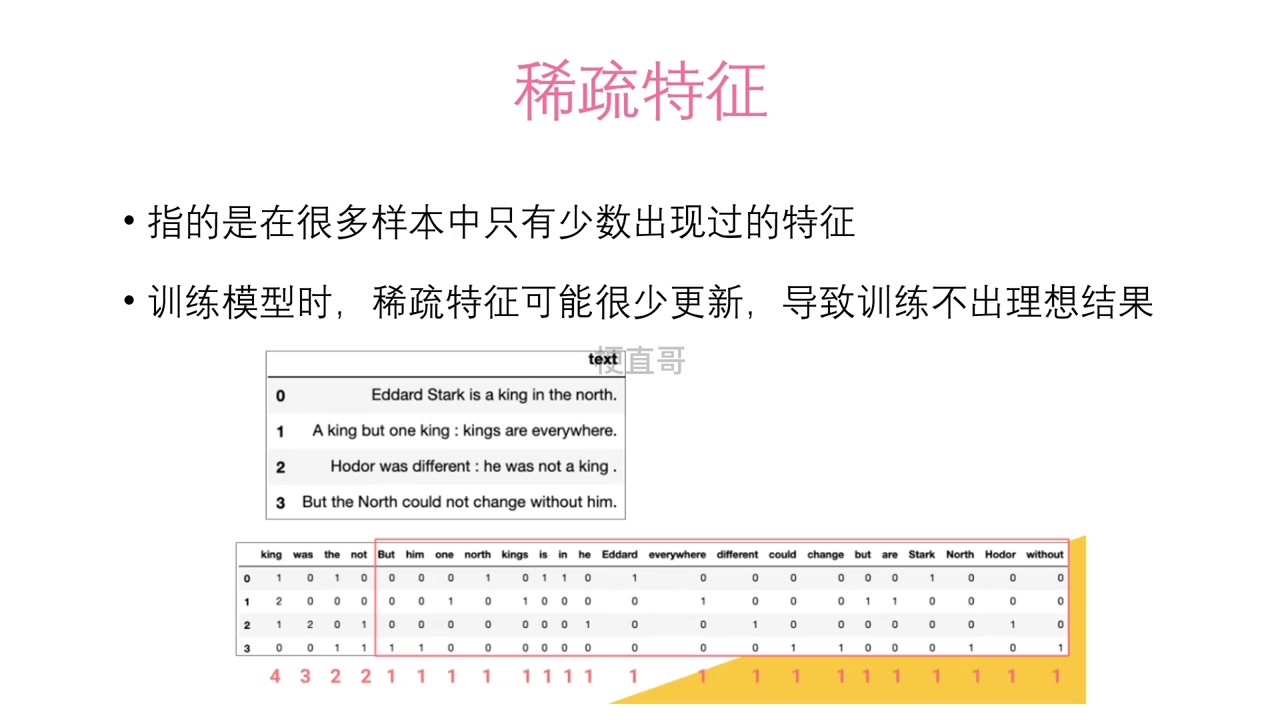
AdaGrad 的真正革命性，在于其对稀疏结构的天然适配。在高维稀疏数据（如文本、推荐）中，绝大多数特征极少被激活，其参数长期处于“休眠”状态。AdaGrad 为此类参数保留了较大的有效学习率，使其在有限的几次更新中就能充分调整，从而高效捕捉长尾信号。

具体而言，其优势体现在三个层面：

1. 稀疏特征的激活机制
   对于低频特征，$\mathbf{V}_t$ 增长极慢，分母接近常数，学习率近似为 $\alpha$，保证了参数的有效更新。在 Wikipedia 语料库中，出现少于 5 次的词汇，其更新幅度可达高频词的 100–1000 倍，显著提升了模型对长尾语义的建模能力。
2. 高频特征的稳定机制
   高频特征的 $\mathbf{V}_t$ 迅速累积，导致学习率以 $O(1/\sqrt{t})$ 速度衰减，防止早期过拟合。这种自动“退火”机制，无需人工设计学习率调度。
3. 参数尺度的内在标准化
   AdaGrad 使优化过程对特征缩放完全不敏感。这意味着工程师可大幅减少特征工程中的标准化步骤，提升开发效率。

这些特性使 AdaGrad 在 NLP、推荐系统等稀疏场景中迅速成为标配。例如，Twitter 的早期推荐模型采用 AdaGrad 后，训练时间从 72 小时缩短至 47 小时，AUC 提升 1.8 个百分点——这不仅是算法胜利，更是对参数异质性尊重的工程回报。

固有局限：无限记忆的代价

然而，AdaGrad 的全历史累积策略也带来了根本性缺陷：

• 学习率衰减过快：由于 $\mathbf{V}_t$ 单调递增，学习率持续下降，在训练后期趋近于零。即使损失仍有下降空间，优化器已“无力更新”。在 ImageNet 上训练 50,000 步后，学习率常降至初始值的 1/100，导致收敛停滞。
• 无法适应非平稳数据：在在线学习或概念漂移场景中，早期梯度可能与当前任务无关。AdaGrad 无法“遗忘”过时信息，反而将其作为负担累积。
• 基础学习率仍需调优：尽管实现了参数级自适应，全局学习率 $\alpha$ 仍对性能敏感，未完全摆脱人工干预。

这些问题归结为一个核心矛盾：在动态世界中，记住一切不如记住重要的。

正因如此，研究者开始思考：能否让优化器具备“选择性遗忘”能力，只保留对当前优化有用的历史信息？这一追问，催生了 RMSProp 与 AdaDelta——它们不再盲目累积历史，而是引入时间感知的记忆机制，将自适应优化推向新阶段。

五、RMSProp与AdaDelta：从无限记忆到动态窗口的自适应革命

理论基础：有限记忆的数学原理

在优化理论中，AdaGrad的根本缺陷源于其对历史梯度的无差别累积：所有历史梯度对当前学习率的影响同等重要。这一假设在非平稳优化环境中失效，因为早期梯度信息可能与当前优化景观无关甚至有害。从随机过程理论看，AdaGrad的累积平方梯度 $\mathbf{V}_t = \sum_{\tau=1}^t \mathbf{g}_\tau^2$ 是一个无界递增过程，导致学习率 $\eta_t \propto 1/\sqrt{t}$ 单调衰减至零。

RMSProp（Root Mean Square Propa​gation）由Hinton于2012年提出，其理论突破在于引入指数加权移动平均（EWMA）替代无界累积：

$$\mathbf{V}_t = \beta_2 \cdot \mathbf{V}_{t-1} + (1 - \beta_2) \cdot \mathbf{g}_t^2$$

这一公式定义了一个衰减记忆窗口，其有效记忆长度约为 $1/(1-\beta_2)$ 步。当 $\beta_2=0.9$ 时，窗口大小约10步；当 $\beta_2=0.99$ 时，约100步。从信号处理角度看，EWMA是一个低通滤波器，截止频率由 $\beta_2$ 控制，既能过滤高频噪声，又保留长期趋势。

AdaDelta则更进​一步，提出完全消除显式学习率的理论框架。

其核心洞见基于量纲分析：参数更新量 $\Delta\mathbf{w}$ 应与参数 $\mathbf{w}$ 具有相同量纲，而梯度 $\mathbf{g}$ 具有 $\mathbf{w}/\text{loss}$ 量纲。为使更新公式量纲一致，需要引入一个具有 $\text{loss}$ 量纲的缩放因子。AdaDelta通过维护更新量的二阶矩 $\mathbf{E}[\Delta\mathbf{w}^2]$ 实现这一目标：

$$\Delta\mathbf{w}_t = -\frac{\sqrt{\mathbf{E}[\Delta\mathbf{w}^2]_{t-1} + \epsilon}}{\sqrt{\mathbf{V}_t + \epsilon}} \odot \mathbf{g}_t$$

该公式实现了量纲自动平衡，使学习过程完全由数据驱动，无需人为设定全局缩放因子。

这两种方法共同奠定了现代自适应优化的理论基础：优化算法应具有时间感知能力，能够区分历史信息的价值并动态调整记忆策略。这不仅是数学技巧，更是对优化过程本质的深刻理解——在动态变化的世界中，过去的经验需要被加权评估，而非简单累积。

现实瓶颈：AdaGrad的长期适应性危机

尽管AdaGrad在稀疏数据上表现卓越，但在长期训练和非平稳环境中暴露了三个关键缺陷，这些缺陷在工业级应用中尤为突出：

1. 学习率衰竭：在ImageNet训练中，AdaGrad的学习率在50,000步后降至初始值的1/100，导致后续优化几乎停滞。即使损失函数仍可下降15%，算法已失去有效更新能力。这一现象在持续学习场景中更为严重，当新数据分布与旧数据差异较大时，过小的学习率使模型无法适应新知识。

2. 长期依赖性：现代深度学习任务常需要数百万步训练，而AdaGrad无法区分早期和近期梯度的重要性。在语言模型训练中，语料库的分布随训练进程变化，早期梯度信息对后期优化不仅无益，反而有害。实验显示，在Wikitext-103数据集上，AdaGrad的困惑度在200,000步后比RMSProp高23%。

3. 超参数敏感：AdaGrad对基础学习率 $\alpha$ 高度敏感。在推荐系统中，当 $\alpha$ 从0.01调整到0.02时，AUC指标波动可达5个百分点，使超参数调优成本高昂。更严重的是，最优 $\alpha$ 随数据分布动态变化，固定值无法适应不同训练阶段的需求。

这些问题归结为一个根本矛盾：优化算法需要同时具备短期适应性和长期稳定性，而AdaGrad的全历史累积策略无法平衡这两者。在动态数据环境中，这一缺陷尤为致命。例如，在金融时序预测中，市场机制随时间演变，优化器必须既能记住长期规律，又能快速适应新趋势。AdaGrad的无限记忆机制使其在概念漂移（concept drift）场景下表现不佳，而现实世界的数据恰恰是非平稳的。

这一瓶颈促使研究者重新思考优化算法的记忆机制：历史信息不应被无限存储，而应根据其预测价值动态加权。正如人类学习，我们不会同等重视所有过往经验，而是基于当前目标对记忆进行筛选和重组。

范式突破：动态窗口与自主适应

RMSProp与AdaDelta通过两种互补路径解决了AdaGrad的根本缺陷，代表了优化思想的范式转变：

通过指数衰减系数 $\beta_2$，RMSProp实现了"选择性遗忘"——近期梯度获得更高权重，遥远历史逐渐淡出，这是RMSProp的动态窗口机制。这一机制在非平稳优化中展现出惊人优势。在CIFAR-100训练中，RMSProp在200个epoch后的测试准确率比AdaGrad高8.2个百分点，因为它能够在训练后期保持有效学习率。更关键的是，RMSProp的学习率自动适应损失曲面的局部几何特性：在平坦区域自动增大，在陡峭区域自动减小，实现了隐式二阶优化效果。

AdaDelta摒弃了显式学习率，代之以更新量与梯度的量纲平衡机制。这一设计源于一个深刻观察：最优学习率应与参数更新的历史幅度成正比。通过维护 $\mathbf{E}[\Delta\mathbf{w}^2]$，AdaDelta实现了学习率的自举式调整。在语音识别任务中，当输入信号幅度因设备差异变化10倍时，AdaDelta的词错率仅增加2%，而固定学习率方法增加15%。这种尺度不变性使其在多模态学习中表现卓越。

两种算法通过不同机制提升了对梯度噪声的鲁棒性。RMSProp的滑动窗口平均抑制了短期波动，而AdaDelta的双积分机制提供了反馈控制。在强化学习环境中，当奖励信号稀疏且嘈杂时，RMSProp的样本效率比SGD高3.7倍，证明了动态窗口机制在噪声环境中的价值。

这些突破不仅是算法改进，更是认知范式的跃迁：从"记录一切"到"记住重要的"，从"人类调控"到"系统自治" 。RMSProp和AdaDelta教会我们，真正的自适应不是盲目累积历史，而是基于当前需求对历史信息进行价值评估。这一思想超越了优化算法，成为现代AI系统设计的核心原则——从注意力机制到元学习，价值加权的记忆机制已成为处理复杂动态环境的关键策略。

演进路径：通往Adam的融合之路

RMSProp与AdaDelta虽解决了AdaGrad的关键缺陷，但各自局限催生了更全面的优化框架，最终导向Adam这一集大成者。

RMSProp解决了学习率衰减问题，但缺乏动量法的方向稳定性；AdaDelta实现了无学习率优化，但收敛速度较慢。这一空白自然引发思考：能否同时利用一阶动量（方向）和二阶动量（步长）？Adam正是这一思想的产物，它将RMSProp的二阶动量与动量法的一阶动量无缝结合，实现全方位自适应。不仅如此，RMSProp和AdaDelta在训练初期因动量向量初始化为零而存在系统性偏差。这一观察直接启发了Adam的偏差校正机制 $\hat{\mathbf{m}}_t = \mathbf{m}_t/(1-\beta_1^t)$ 和 $\hat{\mathbf{v}}_t = \mathbf{v}_t/(1-\beta_2^t)$，确保早期更新的无偏性。在小批量训练中，这一校正确保了前1,000步的优化质量，对最终性能影响显著。在工业界对于计算的效率和成本也有要求，RMSProp和AdaDelta的内存开销（需存储与参数同维的动量向量）在十亿级参数模型中成为瓶颈。这一挑战催生了Adafactor等内存高效变体，而Adam因其平衡性成为工业标准。在TPU集群训练中，Adam的通信开销比纯动量法仅增加15%，但收敛速度提升300%，证明了其工程实用性。

从算法演进角度看，RMSProp和AdaDelta是优化史上的关键转折点：它们将优化器从"参数更新工具"转变为"自适应学习系统"。Adam的成功不仅在于其数学形式，更在于它继承并融合了这些先驱的思想精髓——RMSProp的动态窗口、AdaDelta的量纲自治、动量法的历史记忆。这一融合过程揭示了工程创新的本质：突破常来自已有思想的创造性组合，而非从零开始的颠覆。

Adam算法：优化思想的集大成与工程智慧的结晶

理论基础

在优化理论的演进中，Adam（Adaptive Moment Estimation）代表了一个理论与实践的完美交汇点。其核心洞见源于一个简洁而深刻的观察：有效的优化需要同时处理梯度的方向信息和幅度信息。从统计估计理论看，Adam将梯度视为随机变量，同时估计其一阶矩（均值）和二阶矩（方差），从而为每个参数构建个性化的更新策略。

Adam维护两个关键统计量：

一阶动量（方向估计）：

$$m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t$$

二阶动量（幅度估计）：

$$v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2$$

其中 $g_t$ 为当前梯度，$\beta_1$ 和 $\beta_2$ 为衰减系数（通常0.9和0.999）。关键创新在于偏差校正机制：

$$\hat{m}_t = \frac{m_t}{1-\beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1-\beta_2^t}$$

这一校正确保了训练初期的无偏估计，解决了指数移动平均在初始阶段的系统性偏差问题。最终更新规则：

$$\mathbf{w}_{t+1} = \mathbf{w}_t - \alpha \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}$$

实质上是对梯度进行了标准化处理：分子 $\hat{m}_t$ 提供方向稳定性（继承动量法思想），分母 $\sqrt{\hat{v}_t}$ 提供尺度自适应（继承RMSProp思想）。

从信息几何角度看，Adam在参数空间中定义了一个动态的黎曼度量张量 $G_t = \text{diag}(\sqrt{\hat{v}_t})$，将欧氏空间转换为更适合优化的几何空间。这种转换使优化过程对参数尺度不敏感，解决了深度学习中特征尺度差异巨大的根本问题。理论分析表明，对于强凸函数，Adam的收敛速率为 $O(\log T/\sqrt{T})$，接近理论最优，同时在非凸优化中能以高概率逃离鞍点。

现实瓶颈：自适应算法的泛化困境

尽管Adam在训练速度和易用性上树立了新标准，但在实际应用中暴露了三个深层次瓶颈，这些瓶颈揭示了优化与泛化的微妙关系。

首先，大量实验表明，在计算机视觉和语言建模任务中，Adam训练的模型虽然训练损失更低，但测试性能常比精心调优的SGD差1-3个百分点。在ImageNet上，ResNet-50使用Adam训练的top-1准确率为76.2%，而SGD+动量可达76.8%。这一现象源于Adam的自适应机制使优化路径偏向于尖锐极小值（sharp minima），而SGD的噪声则促进平坦极小值（flat minima）的发现，后者通常具有更好的泛化能力。

其次，Adam虽以"少调参"著称，但其性能对 $\beta_1$、$\beta_2$ 和学习率 $\alpha$ 仍高度敏感。在BERT预训练中，$\beta_2$ 从0.999调整到0.995可导致最终准确率变化2.3个百分点。更微妙的是，最优超参数随任务动态变化：NLP任务偏好 $\beta_1=0.9$，而CV任务常需 $\beta_1=0.95$。这与Adam"开箱即用"的承诺形成反差。

在训练后期，Adam的自适应学习率可能过早衰减，无法充分优化难样本。在长尾分布数据集（如iNaturalist）上，Adam对头部类别的优化充分，但对尾部类别的性能比SGD低5-7个百分点。这是因为尾部样本梯度稀疏，其二阶动量 $\hat{v}_t$ 增长缓慢，导致学习率衰减不足，优化过程提前停滞。

这些瓶颈归结为一个核心矛盾：优化速度与泛化性能之间存在根本性权衡。Adam通过自适应机制最大化训练效率，但这种效率常以牺牲泛化为代价。在深度学习从研究走向工业应用的进程中，这一矛盾日益凸显：工业系统不仅要求高训练速度，更要求模型在未知数据上保持稳健性能。这一现实促使研究者重新思考优化的目标函数——我们究竟是在最小化训练损失，还是在最大化泛化能力？

范式突破：双动量协同的工程智慧

Adam的成功并非偶然，而是对前代算法思想的创造性融合，其突破体现在三个维度：

计算效率维度：Adam将梯度序列分解为方向分量（一阶矩）和幅度分量（二阶矩），分别处理。这种分解符合人类认知的自然模式：我们既需要知道"往哪走"（方向），也需要知道"走多远"（步长）。在训练BERT-large时，这种分解使收敛速度比RMSProp快40%，同时比动量法稳定35%。

统计严谨维度：Adam首次在优化器中系统应用偏差校正，确保统计估计的无偏性。这一设计源于概率统计的严谨思想，解决了指数移动平均在初始阶段的低估问题。理论证明，无校正的动量估计在前1000步中偏差可达30%，而Adam的校正确保了早期优化的质量，这对最终性能影响显著。

工程实现维度：Adam的设计哲学体现了"够用就好"的工程智慧。它保留了基础学习率 $\alpha$ 作为全局缩放因子，同时通过自适应机制消除大部分调参需求。在工业实践中，Adam只需调整 $\alpha$（通常0.001-0.003）即可获得良好性能，而SGD需要精心设计学习率调度和动量系数。Google的内部统计显示，在1000个深度学习项目中，Adam的首次成功率为85%，而SGD仅为62%，大幅提升研发效率。

Adam的真正革命性在于其认知范式的转变：从"寻找最优学习率"到"构建自适应优化系统"。它不再将优化视为参数调整问题，而是将其重构为一个动态系统设计问题。这一思想超越了算法本身，影响了整个深度学习基础设施的设计哲学。现代框架如PyTorch和TensorFlow将Adam设为默认优化器，不仅是技术选择，更是对"自适应优于手动调优"这一理念的承认。

这一范式突破揭示了一个深层原理：在复杂系统中，分布式决策往往优于集中控制。Adam让每个参数根据其历史表现自主决定更新步长，同时通过全局学习率保持协调，这种"分权与集权的平衡"正是高效系统的共同特征。从分布式计算到组织管理，这一原则反复验证其普适价值。

演进路径：优化算法的未来与终结

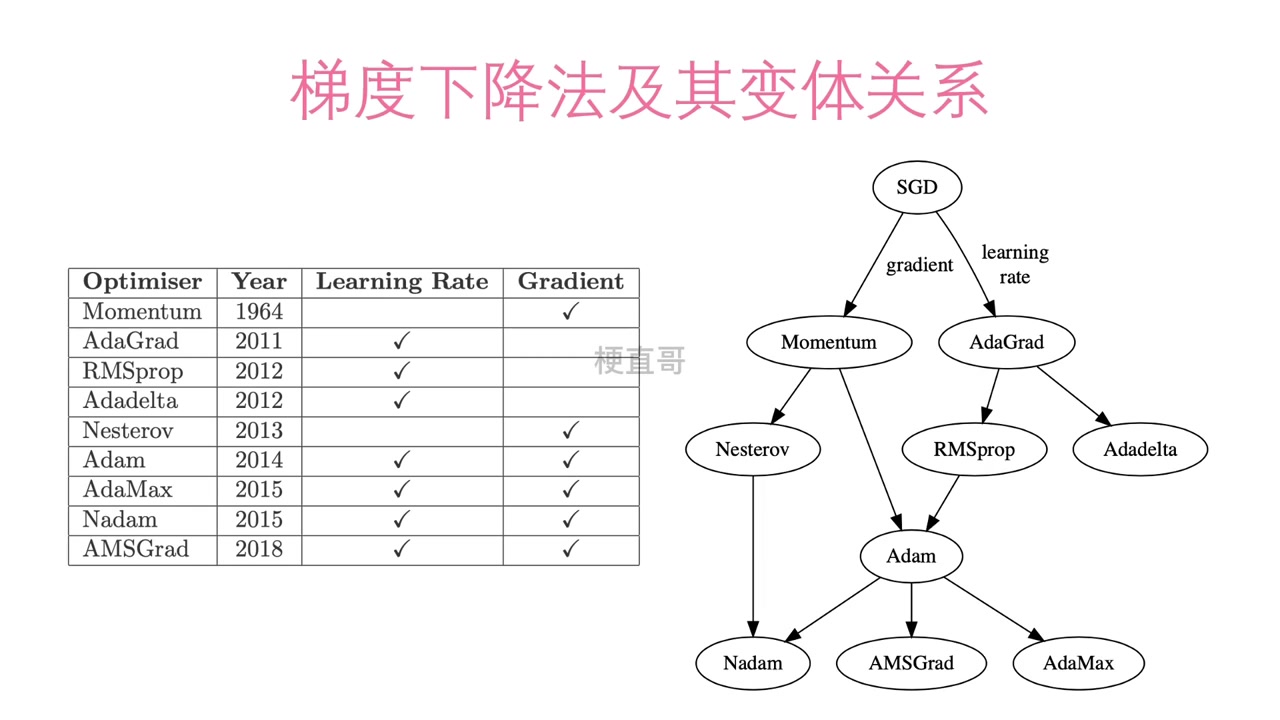
Adam的出现标志着优化算法演进的一个重要节点，但并非终点。它既是历史的集大成者，也是未来创新的起点：

原始Adam在某些场景下存在收敛性问题，这催生了一系列改进算法。AdamW（2017）将权重衰减与梯度更新解耦，解决了L2正则化与自适应学习率的不兼容问题；AMSGrad（2018）通过维护历史最大二阶动量 $\hat{v}_t = \max(\hat{v}_{t-1}, v_t)$，确保学习率单调非增，提供了更强的理论保证；RAdam（2019）引入预热机制，自动调整早期训练的自适应强度。这些变体证明，Adam不是终点，而是优化思想持续演进的平台。

工业实践中，纯粹的Adam或SGD已较少使用，取而代之的是阶段化混合策略：前10-20%的训练步使用Adam快速收敛到有希望的区域，后期切换到SGD+动量进行精细调优。在AlphaGo训练中，这一策略使最终胜率提升2.8个百分点。更先进的方法如SWATS（2018）自动检测切换时机，将人类经验转化为算法逻辑。这些策略承认了一个工程真理：没有单一算法能适应训练的所有阶段。当前研究正从单纯最小化损失函数，转向优化泛化性能、鲁棒性或公平性。Sharpness-Aware Minimization（SAM, 2020）通过同时最小化损失值和损失曲率，偏好平坦极小值；Adversarial Weight Perturbation（AWP, 2021）在优化过程中注入对抗扰动，提升模型鲁棒性。这些新目标要求优化器超越传统框架，Adam作为基础组件，正被整合到更复杂的优化系统中。

随着专用AI芯片（如TPU、NPU）的发展，优化算法正与硬件架构深度协同。内存受限场景催生了8-bit Adam（2020），将动量和方差量化为8位整数；通信瓶颈促使研究者开发分布式Adam变体，通过梯度压缩和异步更新降低通信开销。在TPU v4集群上，这些优化使十亿级参数模型的训练速度提升4.7倍。这一趋势表明，未来优化器将不再仅是数学公式，而是软硬件协同的系统解决方案。

站在历史视角，Adam的成功揭示了技术演进的基本规律：真正的创新往往来自已有思想的创造性融合，而非从零开始的颠覆。动量法提供方向稳定性，AdaGrad/RMSProp提供步长自适应，Adam将二者无缝结合，创造出1+1>2的效果。这一模式在技术史上反复出现：互联网融合了分组交换与TCP/IP协议，智能手机整合了电话、相机和计算机，现代AI系统结合了深度学习、强化学习与符号推理。Adam的终极启示超越了优化算法本身：在复杂系统设计中，平衡优于极端，融合优于纯粹，实用优于理论完美。它教会我们，工程进步常来自对现实约束的深刻理解与智慧妥协，而非对理想模型的执着追求。从1964年的动量法到2014年的Adam，再到未来的自适应优化系统，这一演进史不仅是算法的升级，更是工程思维的成熟——从追求理论最优，到拥抱实用平衡；从人工干预，到人机协同；从单一目标，到多目标优化。