每日三思（5月15日）

问题一：今天学了什么？

今天了解了SVM的基础原理，然后观看了红杉AI Ascent会议

问题二：AI Acsent会议讲了什么？

一、AI 从“不可避免”走向“迫在眉睫”

过去一年，AI 的发展进入快车道。基础设施已经齐备，包括算力、数据、网络、人才和全球分发渠道。与云计算和移动互联网相比，AI 技术的普及更快，覆盖人群更广。ChatGPT 的发布被视为“发令枪”响起，全球用户迅速涌入，AI 的社会关注度与接受度都远高于前几次技术浪潮，门槛也大大降低。

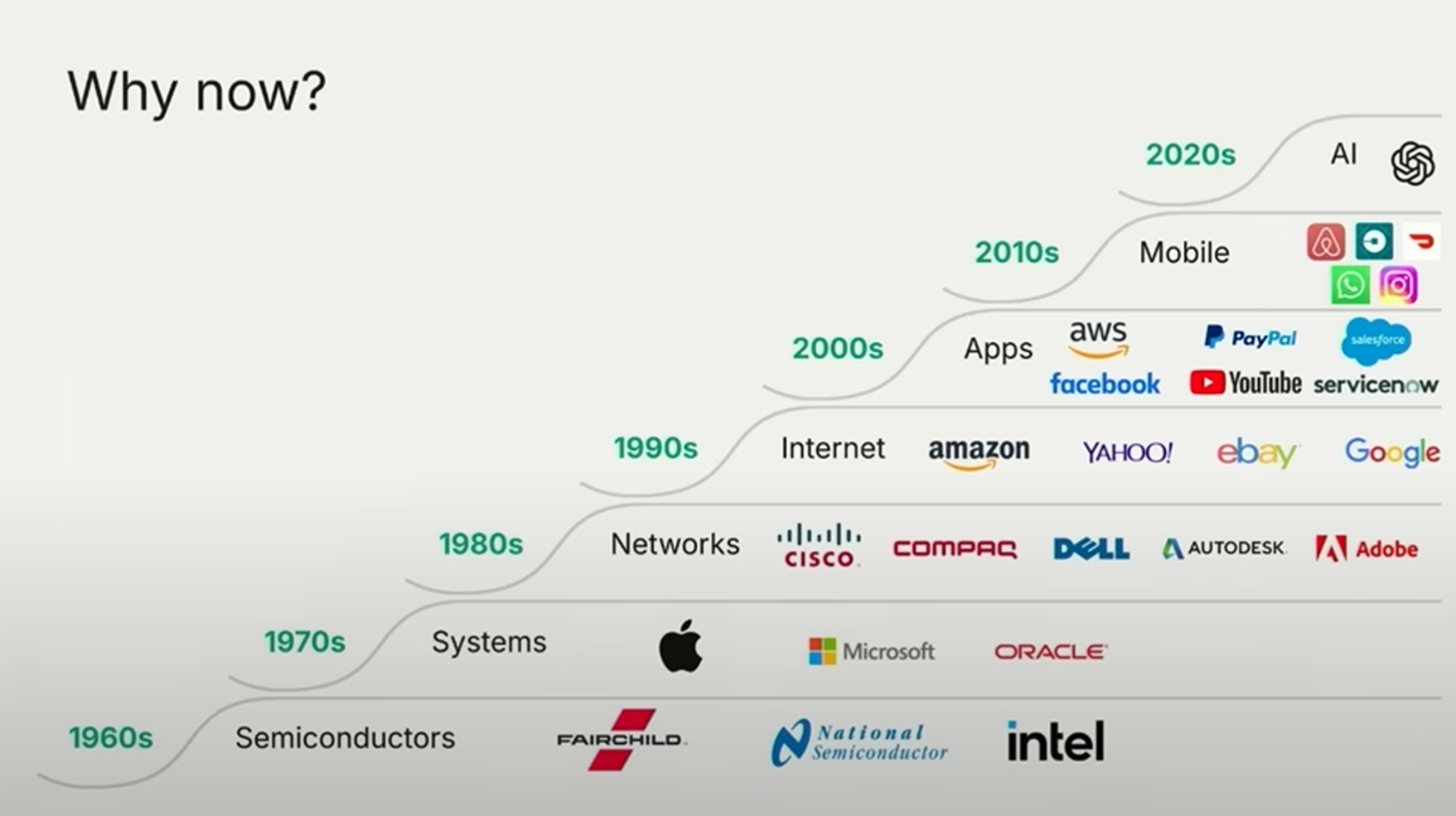
二、AI 同时重塑软件与服务两大市场

AI 应用的商业路径正在发生根本性转变。很多产品从最初作为工具出售，逐步升级为协助执行任务的“协作系统”，最终变成可以完全自动完成任务的“自动驾驶系统”。这意味着收入来源从传统的软件预算，向人力成本预算转移，AI 不仅改变了工作方式，更重塑了价值捕获的方式。

三、应用层仍是价值高地，垂直领域机会巨大

尽管基础模型能力在增强，并逐渐下沉至应用层，但从实际商业价值来看，应用层依旧是最重要的战场。红杉认为，最具竞争力的创业公司往往不是从技术出发，而是从客户问题出发，反向构建垂直化、行业专属、功能聚焦的解决方案。这类产品可以通过流程整合、人机协作、数据闭环形成护城河，建立持续领先优势。

四、衡量 AI 创业公司成功的三个关键指标

第一是收入质量，必须区分真实用户价值带来的收入，还是仅为测试产品或跟风尝鲜而产生的“气氛营收”。第二是毛利率路径，虽然初期算力成本高，但随着模型推理成本持续下降，加上产品价值提升，未来毛利可期。第三是数据飞轮，必须明确数据机制是否真正推动核心业务指标，否则只是噱头。

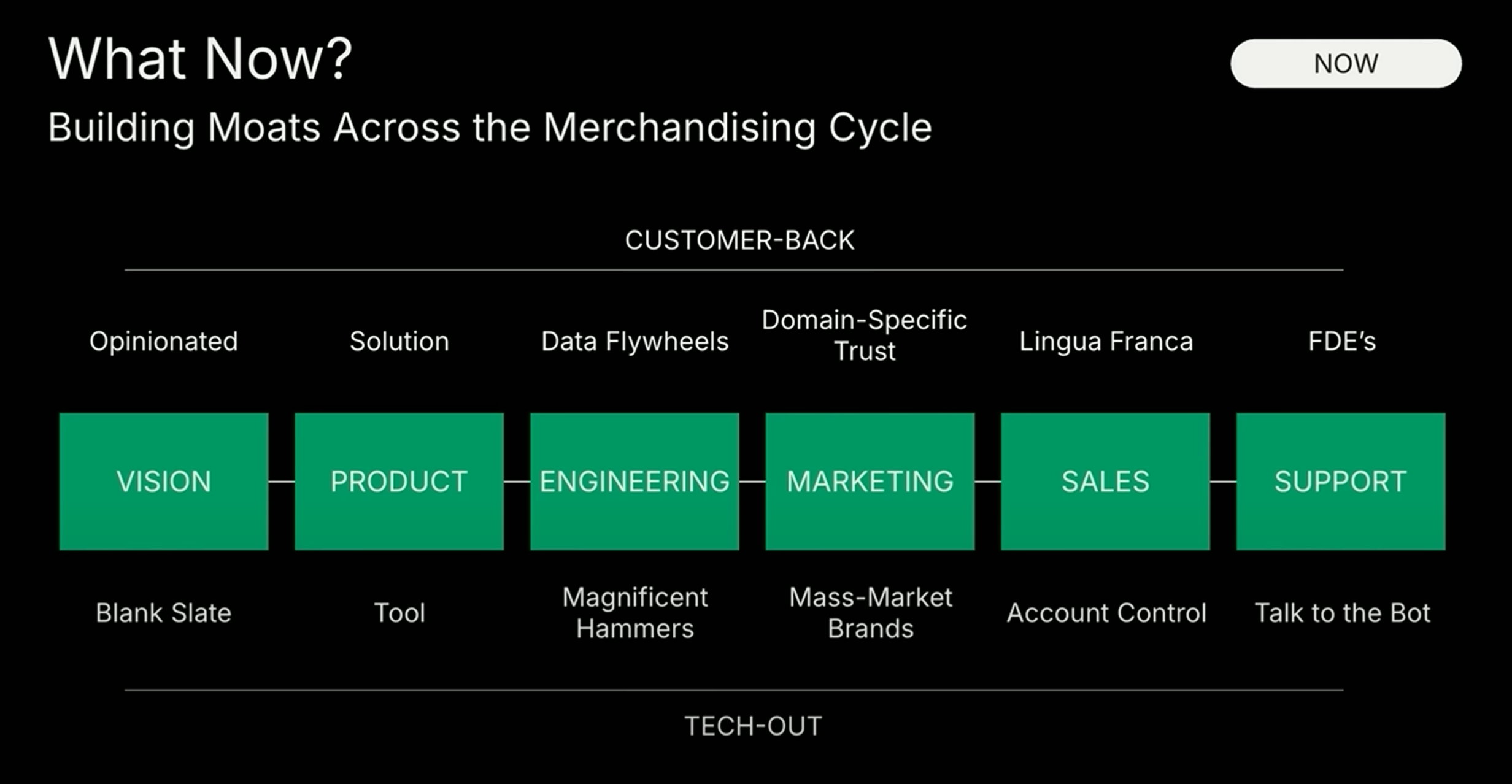
五、AI 应用进入用户日常生活，多个行业已率先爆发

用户活跃度显著提升，ChatGPT 的活跃度已接近 Reddit。应用落地层面，语音生成已跨越“恐怖谷”，代码生成工具进入主流，医疗、广告、教育等领域也出现了极具爆发力的创新产品。AI 不再只是科技圈的探索，而是正逐步嵌入每个普通人的日常工作与生活中。

六、AI 代理（Agent）是下一波重大浪潮

继独立智能体之后，出现了智能体网络（Agent Swarms），多代理协作处理复杂任务。红杉预测未来将进入“代理经济”阶段，代理不仅传递信息，还将执行任务、管理资源、建立信任、完成交易。这将极大重塑人与机器的关系，不是取代人，而是与人协作共生。

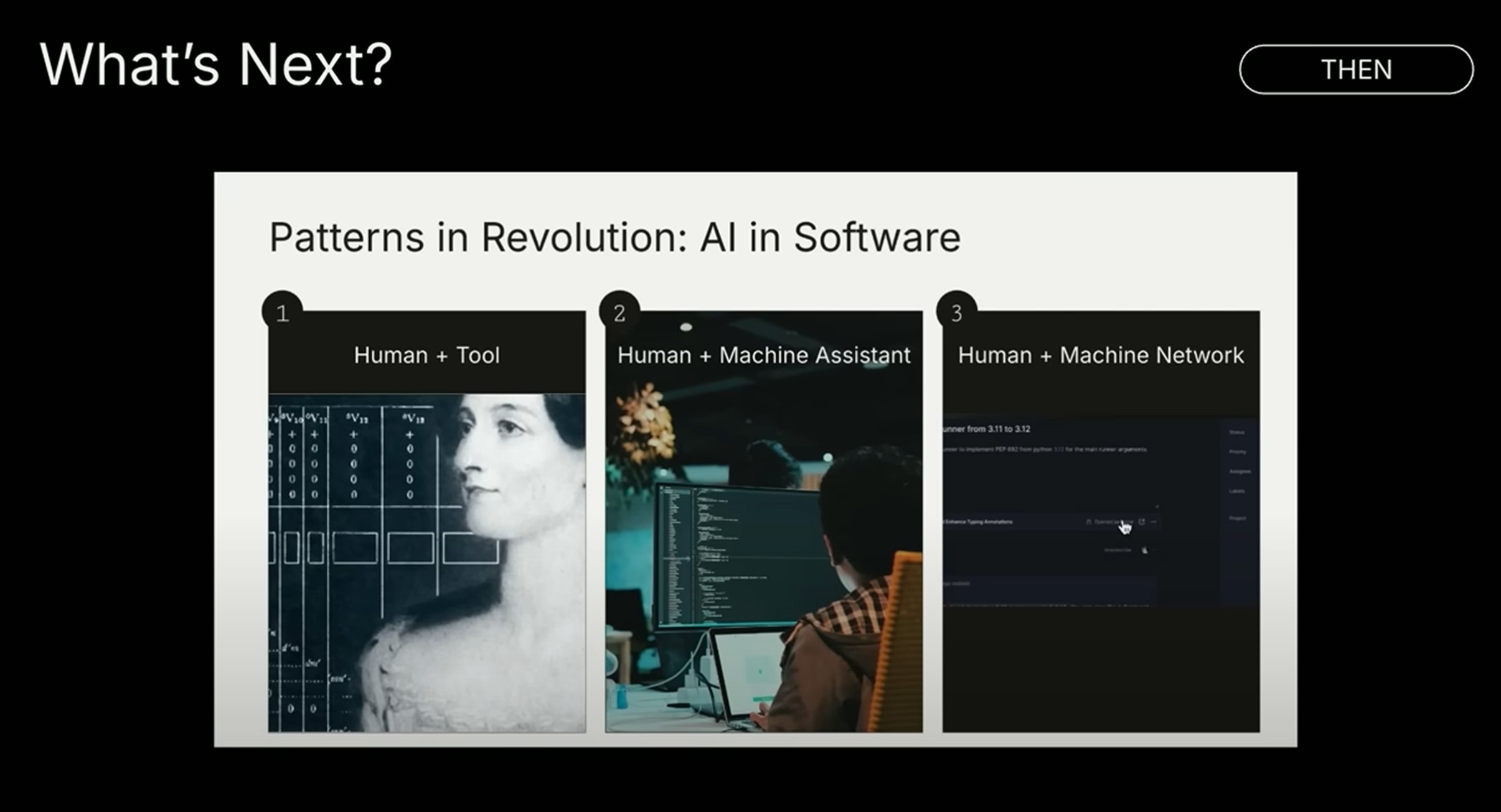
七、构建代理经济的三大技术基础

首先是身份持久性，代理需要持续保持自己的行为一致性，并长期记住用户信息。其次是通信协议的标准化，类似于 TCP/IP 之于互联网，目前 MCP 等协议初具雏形。最后是安全性，未来人与代理之间的协作高度依赖身份验证、访问控制和信任机制，安全将成为核心保障。

八、AI 正在重构个体的工作模式与组织形态

人们需要适应从确定性计算向随机性计算的思维转变，这是所谓“随机性思维”，即系统可能会做出不同响应，但整体仍然有效。个体也将从执行者变为管理者，未来大多数人将学会如何高效地指挥和协作 AI，而不是亲自完成每一项任务。这将极大提升杠杆率，但也对风险管理提出更高要求。

九、AI 正在推动“丰裕时代”的到来

AI 大幅降低了创造内容、开发软件的门槛与成本，未来劳动力将变得“便宜而充足”。真正稀缺的能力将不再是能不能做，而是做得好不好——判断力、审美、品味成为竞争焦点。这种转变将深刻影响产品、服务、管理和组织的演化路径。

问题三：SVM的基本原理是什么？

SVM（支持向量机，Support Vector Machine）是一种经典的监督学习算法，主要用于分类任务，也可以用于回归和异常检测。它通过寻找最大间隔分类边界来实现高效分类的机器学习方法，适用于中小规模数据集。

一、SVM 的核心原理

SVM 的目标是找到一个最优的分界线（超平面） ，将不同类别的数据尽可能清晰地分开。

关键概念：

一、间隔最大化（Margin Maximization）

SVM 的目标是找到一个最优超平面，将两类数据尽可能分开，并使分类间隔最大。

基本形式：

假设超平面为：

$$\mathbf{w} \cdot \mathbf{x} + b = 0$$

其中：

• $\mathbf{w}$ 是法向量（决定超平面方向）
• $b$ 是偏置项
• $\mathbf{x}$ 是输入样本点

对于线性可分的数据，我们希望满足以下约束：

$$y_i(\mathbf{w} \cdot \mathbf{x}_i + b) \geq 1 \quad \text{(对所有样本 i)}$$

分类间隔公式：

分类间隔（margin）为：

$$\text{Margin} = \frac{2}{\|\mathbf{w}\|}$$

最优化问题：

SVM 的目标是最小化 $\frac{1}{2}\|\mathbf{w}\|^2$，在上述约束下求解最优 $\mathbf{w}$ 和 $b$。

这是一个典型的带约束的最优化问题，通常用拉格朗日乘子法求解。

二、支持向量（Support Vectors）

支持向量是指那些距离分类边界最近的样本点，它们决定了最终的分类边界。

数学表达：

在求解过程中，引入拉格朗日乘子 $\alpha_i$，只有对应的支持向量其对应的 $\alpha_i > 0$，其余样本的 $\alpha_i = 0$。

最终决策函数为：

$$f(\mathbf{x}) = \sum_{i=1}^n \alpha_i y_i (\mathbf{x}_i \cdot \mathbf{x}) + b$$

其中，$\alpha_i > 0$ 的样本就是支持向量。

三、核技巧（Kernel Trick）

当数据不是线性可分时，通过核函数将原始空间映射到高维空间，使其变得线性可分。

核函数定义：

核函数 $K(\mathbf{x}_i, \mathbf{x}_j)$ 表示两个样本在高维空间中的内积：

$$K(\mathbf{x}_i, \mathbf{x}_j) = \phi(\mathbf{x}_i) \cdot \phi(\mathbf{x}_j)$$

其中 $\phi(\cdot)$ 是映射函数。

常见核函数公式：

核函数名称	公式
线性核（Linear Kernel）	$K(\mathbf{x}_i, \mathbf{x}_j) = \mathbf{x}_i \cdot \mathbf{x}_j$​
多项式核（Polynomial Kernel）	$K(\mathbf{x}_i, \mathbf{x}_j) = (\gamma \mathbf{x}_i \cdot \mathbf{x}_j + r)^d$​
RBF 核 / 高斯核（Radial Basis Function Kernel）	$K(\mathbf{x}_i, \mathbf{x}_j) = \exp(-\gamma |\mathbf{x}_i - \mathbf{x}_j|^2)$​

其中：

• $\gamma > 0$：控制核函数“宽度”
• $r$：常数项
• $d$：多项式的阶数

二、SVM 主要用来做什么

1. 分类任务： 如图像识别、文本分类、垃圾邮件检测等。
2. 回归预测（称为 SVR）： 预测连续值，如房价、温度变化等。
3. 异常检测： 检测偏离正常模式的数据点，用于欺诈检测、设备故障诊断等。

三、SVM 的优点和缺点

SVM对小样本和高维数据有较好的分类性能。适合处理图像、文本等复杂数据。但是训练时间长，尤其在大规模数据集上效率较低；对参数选择（如核函数、正则化参数）敏感，需要调参。并且不太适合噪声多或类别重叠严重的数据。