每日三思（5月6日）

问题一：今天学了什么？

今天我在机器学习部分学习了多分类问题以及出现类别不平衡问题时的处理方法，将线性模型的理论部分完成，并且学习了决策树以及其在划分选择中的基本原理。还通过练习掌握了C++中的排序方法：sort​。在拓扑方面，今天对离散morse函数有所了解，但是还是有些模糊，计划找时间重听后再进行单独总结。

问题二：简单介绍一下 sort​ 的基本用法？

首先sort函数一定是bool类型，它的compare函数名不重要，但需要保持和sort的第三个参数一致。自定义的两个参数类型也需要和和容器元素一致。以下是一个实现奇数从大到小排序，偶数从小到大排序的例子。

bool compare(int lhs, int rhs) {
	if (lhs % 2 == 1 && rhs % 2 == 0) {
		return true;
	}
	else if (lhs % 2 == 1 && rhs % 2 == 1 && lhs > rhs) {
		return true;
	}
	else if (lhs % 2 == 0 && rhs % 2 == 0 && lhs < rhs) {
		return true;
	}
	else {
		return false;
	}
}
int main() {

	int arr[10];
	for (int i = 0;i < 10; ++i) {
		scanf("%d", &arr[i]);
	}
	sort(arr, arr + 10, compare);                   //arr本是数组，但作为函数名时，会退化成为指针
	for (int i = 0;i < 10; ++i) {
		printf("%d", arr[i]);
	}
	printf("\n")
	return 0;
}

​sort​ 也可以对 vector​ 进行排序：

sort(vec.begin(),vec.end(),compare); //这里的vec是迭代器

问题三：对决策树模型的理解？

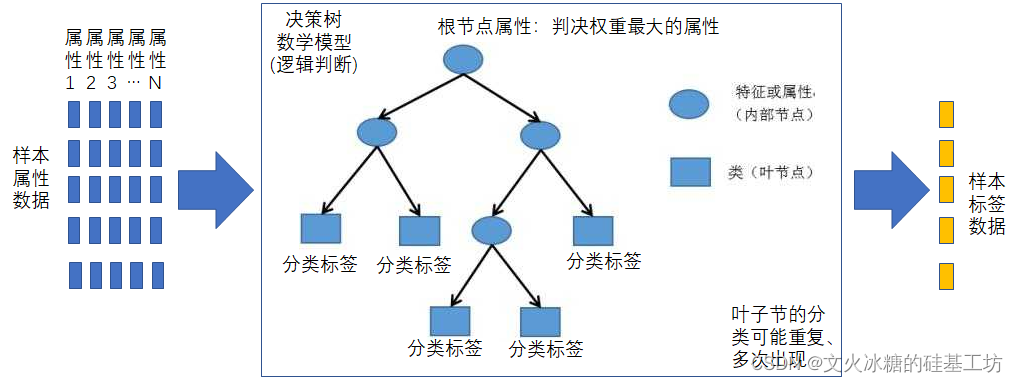
决策树是一种监督学习算法。它的内部节点是该模型的特征属性，叶节点是决策结果。对于决策树模型，最重要的三个问题是：

1. 特征选择
2. 节点分裂
3. 阀值确定

线性模型包含线性回归和Logistics回归本质上还是通过距离这一指标来进行结果的预测或者划分。对于决策树则是通过多个维度进行选择最终输出结果。

问题四：怎么理解熵，以及它为什么会运用于决策树模型？

怎么理解熵？

在信息论中，熵表示一个系统的不确定性或混乱程度 ，熵越大，代表这个系统越混乱。在分类任务中，熵可以用来衡量一个样本集合的“纯度”：

• 如果一个数据集里所有样本都属于同一类 →很“纯净”，熵为 0。
• 如果各类样本混杂在一起 → 很“混乱”，熵很大。

为什么用于决策树？

决策树的目标是通过特征划分数据，使得每一层划分后子集尽可能“纯净”。这就引出了一个重要概念：信息增益.

$$\text{Gain}(S, A) = H(S) - \sum_{v \in V} \frac{|S_v|}{|S|} H(S_v)$$

其中：

• $S$ 是当前的数据集。
• $A$ 是某个特征。
• $S_v$ 是按照特征 $A$ 的第 $v$ 个取值划分出的子集。
• $H(S)$ 是当前数据集的熵。
• $H(S_v)$ 是每个子集的熵。
• $|S_v|$ 和 $|S|$ 分别是子集 $S_v$ 和数据集 $S$ 的大小。

我们可以通过分别计算使用不同特征（如天气、温度、湿度等）的信息增益，选择信息增益最大 的那个特征作为分裂节点。这个特征能最大程度地减少不确定性，使分类更清晰。